- #1
Mech_LS24
- 148
- 16
- TL;DR Summary
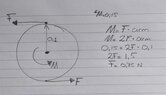
- Just a want to have an indication how much torque I need for rotating a plateau with 7.5 kg. See sketch for clearer view.
Hi!
I would like to calculate (roughly) how much torque is needed bringing the blue plateau in movement. Assume the blue plateau is loaded with 7.5 kg. The radius of the blue circle is 100 mm.

I would like to calculate (roughly) how much torque is needed bringing the blue plateau in movement. Assume the blue plateau is loaded with 7.5 kg. The radius of the blue circle is 100 mm.