Torsion pendulum in Cavendish experiment

[Yoonique]

Homework Statement

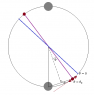
In the Cavendish experiment, the two small balls have mass m each and are connected by a light rigid rod with length L. The two large balls have mass M each and are separated by the same distance L. The torsion constant of the torsion wire is κ.
b) Put the large balls a small distance away from the small balls, when the system reaches the equilibrium, the rigid rod rotates an angle θ and the distance between the centers of balls is r, as shown in the above figure. Find the expression for the gravitational constant G.
c)If the small balls are perturbed with small angle from the equilibrium position in (b), will the oscillation be harmonic? If so, find the expression for the period of the oscillation.

Homework Equations

∑τ = Iα
T = 2π/ω

The Attempt at a Solution

I solved for part b. But I can't get the answer to part c.

Part b: G = 2π²Lr²θ/(MT²)

Part c:
Let the new angle be θ₁
∑τ = Iα
GMmL/(r-0.5θcosθ₁)² - κθ₁ = Iα
α = 2GM/(L(r-0.5θcosθ₁)²) - 2κθ₁/(mL²)
I can't make α=-ω²θ₁ to find for ω to solve for T.

 

[paisiello2]

Isn't "r" a function of L and θ?

 

[Yoonique]

Isn't "r" a function of L and θ?

Originally when it is in equilibrium, the distance between M and m is r. Then the small balls are perturbed with small angle from the equilibrium position, so the new distance between M and m is r-0.5θcosθ.

 

[paisiello2]

That's not how I interpret the diagram which clearly shows r depending on the angle θ.

The distance between M and m at equilibrium when θ=0° is r=L/√2.

 

[Yoonique]

That's not how I interpret the diagram which clearly shows r depending on the angle θ.

The distance between M and m at equilibrium when θ=0° is r=L/√2.

In part b it says it rotates at an angle θ when it reaches equilibrium. Then in part c it says the small balls are perturbed with small angle from the equilibrium position in part b. So in part c, the new angle isn't it θ+small angle, which we call it θ₁. I'll edit my θ in my workings to θ₁. I think it's confusing to use the same θ.

 

[paisiello2]

OK, I see that now.

This expression is not correct:
r-0.5θcosθ₁

For one thing the dimensions are wrong.

Since θ₁ is a small angle then a good approximation for the distance between M and m would be:
r' = r-Lθ₁

Now you are squaring this number r'. How much different will r² be from r'²?

 

[Yoonique]

OK, I see that now.

This expression is not correct:
r-0.5θcosθ₁

For one thing the dimensions are wrong.

Since θ₁ is a small angle then a good approximation for the distance between M and m would be:
r' = r-Lθ₁

Now you are squaring this number r'. How much different will r² be from r'²?

Why is it Lθ and not θL/2? Since the radius is L/2.

 

[paisiello2]

Yes, you're right, L/2.

 

[Yoonique]

Yes, you're right, L/2.

So the new torque would be:
2GMm/(r-0.5Lθ₁)₂(L/2) - κθ₁ = Iα
The answer involves a cosθ and it is not in terms of G. Means I got to use part b answer?

 

[paisiello2]

No, do you know how to solve differential equations?

 

[Yoonique]

No, do you know how to solve differential equations?

How do I make it into a differential equation? I think I know how to solve them if it is those basic ones.

Edit: Means I got to change α into d²θ/dt²? And solve it so that I will get an equation relating θ and T?

 

[paisiello2]

Yes, you got it. The only trick is to simplify the equation by assuming (r-0.5Lθ₁)² is approximately r² for small θ₁.

 

[Yoonique]

Yes, you got it. The only trick is to simplify the equation by assuming (r-0.5Lθ₁)² is approximately r² for small θ₁.

It will become 2(GMm/r² - κθ₁) = Lm(d²θ₁/dt²). How do you solve this? It is not linear and homogeneous.

 

[paisiello2]

I think it's linear. Regardless, you only need to come up with the period. So why not assume θ₁ is in the form of a simple harmonic equation?

 

[Yoonique]

I think it's linear. Regardless, you only need to come up with the period. So why not assume θ₁ is in the form of a simple harmonic equation?

I tried re-arranging the equation into the form of α = -ω²θ so that I can use T = 2π/ω. But I can't separate out θ₁ away from the other terms.

 

[paisiello2]

Can you solve the homogenous version of this equation?

 

[Yoonique]

Can you solve the homogenous version of this equation?

I'm not sure how though. Maybe I haven't learn how to solve this type of differential equations. Is differential equation the only way to solve it?

 

[paisiello2]

Afraid so.

 

[Yoonique]

Afraid so.

Can you guide me on using differential equation to solve it?
The equation I have now is 2(GMm/r² - κθ₁) = Lm(d²θ1/dt²)

 

[paisiello2]

First do what I said in post # 12.

 

[paisiello2]

OK, I see that you did that already.

 

[Yoonique]

OK, I see that you did that already.

Yeah, how do I continue from there? How do I alter the equation so I can integrate them?

 

[TSny]

I tried re-arranging the equation into the form of α = -ω²θ so that I can use T = 2π/ω. But I can't separate out θ₁ away from the other terms.

The net torque may be written $$\tau = \frac{A}{r^2} - \kappa \theta = \frac{A}{(r_0- b\, \delta \theta)^2} - \kappa (\theta_0 +\delta \theta) $$ where $A$ and $b$ are constants.

$r_0$ and $\theta_0$ are the equilibrium values of $r$ and $\theta$, and $\delta \theta$ represents displacement of $\theta$ from equilibrium.

For small $\delta \theta$ you can linearize this expression to get $\tau = -B \, \delta \theta$ for some constant $B$.

 

[paisiello2]

You're right, we forgot the original Kθ term. That will simplify the equation down to:

GMm/r² + K(θ+θ₁) = Iθ₁''

(GMm/r² + Kθ) + Kθ₁ = Iθ₁''

Kθ₁ = Iθ₁''

 

[paisiello2]

If we have simple harmonic motion then we can assume that the solution to the differential equation will take the form:

θ₁= A⋅sin(ωt) where A and ω are constants to be determined.

 

[Yoonique]

You're right, we forgot the original Kθ term. That will simplify the equation down to:

GMm/r² + K(θ+θ₁) = Iθ₁''

(GMm/r² + Kθ) + Kθ₁ = Iθ₁''

Kθ₁ = Iθ₁''

Why did you ignore (GMm/r² + Kθ)?

 

[Yoonique]

The net torque may be written $$\tau = \frac{A}{r^2} - \kappa \theta = \frac{A}{(r_0- b\, \delta \theta)^2} - \kappa (\theta_0 +\delta \theta) $$ where $A$ and $b$ are constants.

$r_0$ and $\theta_0$ are the equilibrium values of $r$ and $\theta$, and $\delta \theta$ represents displacement of $\theta$ from equilibrium.

For small $\delta \theta$ you can linearize this expression to get $\tau = -B \, \delta \theta$ for some constant $B$.

So B/I is ω²?

 

[Yoonique]

If we have simple harmonic motion then we can assume that the solution to the differential equation will take the form:

θ₁= A⋅sin(ωt) where A and ω are constants to be determined.

How do I determine the constants when I do not have any values to sub into the equation?

 

[TSny]

So B/I is ω²?

Yes.

Once you find B, you will see that there is an approximation you can make to simplify B.

 

[Yoonique]

Yes.

Once you find B, you will see that there is an approximation you can make to simplify B.

Okay, but I have a problem. I do not know how to linearize it for the fact that δθ is small. What is the trick here? I mean a lot of the post here tells me to 'simplify it' but I just don't know how to get started. I know (r₀ - bδθ)² ≈ r₀ right?

 

[TSny]

Okay, but I have a problem. I do not know how to linearize it for the fact that δθ is small. I know (r₀ - bδθ)² ≈ r₀ right?

That's going too far in the approximation.

For $\frac{1}{(r_0-b \, \delta \theta)^2}$, use the binomial approximation: http://en.wikipedia.org/wiki/Binomial_approximation

 

[Yoonique]

That's going too far in the approximation.

For $\frac{1}{(r_0-b \, \delta \theta)^2}$, use the binomial approximation: http://en.wikipedia.org/wiki/Binomial_approximation

So for this question I just got to approximate properly and I can solve for ω? I do not need differential equation?

 

[TSny]

So for this question I just got to approximate properly and I can solve for ω? I do not need differential equation?

That's right. To first order in $\delta \theta$ the differential equation would be the SHM equation $I \ddot{\delta \theta} = -B \delta \theta$.

So, as you said, $\omega^2 = \frac{B}{I}$.

 

[Yoonique]

That's right. To first order in $\delta \theta$ the differential equation would be the SHM equation $I \ddot{\delta \theta} = -B \delta \theta$.

So, as you said, $\omega^2 = \frac{B}{I}$.

Okay I got (GMmL/2)(r₀^-2 + Lδθr₀^-3) - κ(θ₀+δθ). How can I simplify even further?

 

[TSny]

Okay I got (GMmL/2)(r₀^-2 + Lδθr₀^-3) - κ(θ₀+δθ). How can I simplify even further?

I don't get the 2 in the numerator of the first factor.

To simplify further, think about the condition that holds at equilbrium.

 

[Yoonique]

I don't get the 2 in the numerator of the first factor.

To simplify further, think about the condition that holds at equilbrium.

Isn't the 2 factor because the radius of the circle is L/2?
At equilibrium, GMmL/(2r₀²) = κθ₀. So I sub it in. I'll get -δθ(κ - κθ₀/r₀) = Iα
So ω² = 2κ(r₀ - θ₀)/(mL²r₀).
Therefore T = 2π√(mL²r₀)/2κ(r₀ - Lθ₀)

But my given answer is T = 2π√(mL²r₀)/2κ(r₀ - Lθ₀cosθ₀). Why is there an extra cosθ₀ ...

 

[Yoonique]

If I work backwards, when it is θ = θ₀ + δθ the distance between M and m is (L/2)δθcosθ₀. I thought since δθ is small, I can approximate the distance between M and m as (L/2)δθ?

 

[TSny]

Isn't the 2 factor because the radius of the circle is L/2?

Did you take into account that there are 2 gravitational forces acting on the rod?

At equilibrium, GMmL/(2r₀²) = κθ₀.

OK, except for that factor of 2. (Hope I'm not the one who's dropping a factor of 2 somewhere.)

So I sub it in. I'll get -δθ(κ - κθ₀/r₀) ...

Note that the second term in parentheses does not have the correct dimensions.

 

[Yoonique]

Did you take into account that there are 2 gravitational forces acting on the rod?OK, except for that factor of 2. (Hope I'm not the one who's dropping a factor of 2 somewhere.)Note that the second term in parentheses does not have the correct dimensions.

Ops, is a typo, I forgot about the L inside. It should be δθ(κ - Lκθ₀/r₀). My final answer is T = 2π√(mL²r₀)/2κ(r₀ - Lθ₀). However the given answer is T = 2π√(mL²r₀)/2κ(r₀ - Lθ₀cosθ₀). Why is there an extra cosθ₀? If I work backwards, when it is θ = θ₀ + δθ the distance between M and m is (L/2)δθcosθ₀. I thought since δθ is small, I can approximate the distance between M and m as (L/2)δθ?

 

[paisiello2]

cosθ₀≅1 for small θ₀

 

[Yoonique]

cosθ₀≅1 for small θ₀

But is θ₀ small? Because the question did not state that though. They only state that δθ is small. θ₀ is the equilibrium point though..

 

[haruspex]

cosθ₀≅1 for small θ₀

If cosθ₀ figures in the given answer then clearly θ₀ is not considered small enough to use that approximation.

 

[Yoonique]

If cosθ₀ figures in the given answer then clearly θ₀ is not considered small enough to use that approximation.

Then why is there an extra cosθ₀ in the given answer? Do you know?

 

[haruspex]

Then why is there an extra cosθ₀ in the given answer? Do you know?

No. I haven't tried to follow all the algebraic developments in the thread. I attempted the problem from scratch and got the given answer except that in place of the cosθ₀ I get $\cos(\phi)$, where $r_0 = L \sin(\phi)$. θ₀cosθ₀ feels wrong. I don't see how cosθ₀ could come into it. So I suspect a typo in the given answer.

 

[Yoonique]

No. I haven't tried to follow all the algebraic developments in the thread. I attempted the problem from scratch and got the given answer except that in place of the cosθ₀ I get $\cos(\phi)$, where $r_0 = L \sin(\phi)$. θ₀cosθ₀ feels wrong. I don't see how cosθ₀ could come into it. So I suspect a typo in the given answer.

So the distance between M and m is r₀ - Lδθcos(θ₀/2)/2, where $\cos(\phi)$ = cos(θ₀/2) because it is the angle at the circumference.
But why is the distance m moved is Lδθcos(θ₀/2)/2 not Lδθ/2 since δθ is small.

 

[haruspex]

So the distance between M and m is r₀ - Lθ₀cos(θ₀/2), where $\cos(\phi)$ = cos(θ₀/2) because it is the angle at the circumference.

Whoa, what do you think θ₀ stands for? Isn't it the angle the torsion fibre had turned through to reach the r₀ position? Why would that relate to the angle that m and M subtend at the rod's centre in the equilibrium position?

 

[Yoonique]

Whoa, what do you think θ₀ stands for? Isn't it the angle the torsion fibre had turned through to reach the r₀ position? Why would that relate to the angle that m and M subtend at the rod's centre in the equilibrium position?

Oh I see what you meant. So when m moves an angle of δθ, the distance between M and m is r₀ - δθL/2 right? Which means LsinΦ - δθL/2? But this will give me the answer without the cosΦ. How do you get the cosΦ in the answer? If I worked backwards from the answer, why when m moves an angle of δθ, m moves cosΦ⋅δθL/2?

 

[TSny]

How do you get the cosΦ

The small mass can be thought of as moving along a tangent to the circle, whereas r cuts across the circle. So the motion of the mass and r are not in the same direction.

I agree with haruspex's answer.

 

[Yoonique]

The small mass can be thought of as moving along a tangent to the circle, whereas r cuts across the circle. So the motion of the mass and r are not in the same direction.

I agree with haruspex's answer.

Okay, so the length of the tangent is δθL/2. But I can't visualise why cosΦ⋅δθL/2 will be in the same direction as r.

 

[TSny]

Okay, so the length of the tangent is δθL/2. But I can't visualise why cosΦ⋅δθL/2 will be in the same direction as r.

See figure.