AROD
- 18
- 0
Homework Statement
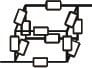
I have a network of resistors in a box-formation. There is 1 resistor of equal resistance in between every corner of the box, so 12 in total.
Homework Equations
In series R = r1 + r2 + ... ri
In parallel, 1/R = 1/r1 + 1/r2 + ... 1/ri
The Attempt at a Solution
I can't really draw a 2D analogous network due to the connections. I know kirchhof's rules must be applied somehow... that no current will flow between two points of equal potential difference, but not sure where that would be.