Trailer being pulled, where to put origin re: torque?

[lizzyb]

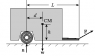
Hi. This question is mostly done by a figure; we have a loaded truck of weight W being pulled by a truck with a force F. The CM point on the figure ndicates the location of the center of mass of the trailer and its load.

Suppose the trailer accelerates forward (a>0) or backwards (a<0). What is the vertical component F_y of the force F on the trailer?

For the forces in the X and Y I have:
$$\sum F_x = ma$$ (since there is some acceleration)
$$\sum F_y = n + F_y - W = 0$$

Now, I suppose, I'm to write an equation for the torque, but this one isn't that easy - where do i put the origin? thank you.

 

[lizzyb]

i don't know if the image will be approved too soon or not; here it is:
http://img233.imageshack.us/my.php?image=10homeworkimage01mx9.png"
if anyone can help with this, that'd be great! :-)

 

[OlderDan]

It's usually a good idea when you have an unknown force to calculate torque relative to the point of application of that force (maybe other places too, but at least at that point). This problem does not involve any driving force at the wheel, so the only force at the wheel is normal to the ground as shown in the diagram.

Edit: This was the wrong approach for this problem. See the later posts.

 

[lizzyb]

do you mean put the origin at the center of the wheel? or do you mean put the origin right where the F vector (the one pulling the cart) is pointing off into space?

if i put the origin at the center of the wheel, aren't i supposed to go through the center of mass and if so, how can i include the force vector?

if i put the origin where the F vector goes off into space, how can I include the normal force?

thanks!

 

[OlderDan]

I mean put the origin where F is acting. You know the direction and the distances from this point for the other forces acting (n and W). This will tell you the relationship between n and W. You already have the equation that relates n, W and F_y.

Edit: This was the wrong approach for this problem. See the later posts.

 

[lizzyb]

I mean put the origin where F is acting. You know the direction and the distances from this point for the other forces acting (n and W). This will tell you the relationship between n and W. You already have the equation that relates n, W and F_y.

so it would be:
$$\sum \tau = w(L - d) - n L = 0$$

So,
$$F_y = w - n = w - \frac{w(L - d)}{L} = \frac{L w - w(L - d)}{L} = \frac{w(L - L + d)}{L} = \frac{wd}{L}$$

hmm, the answers to choose from are things like $$F_y = \frac{W}{2L}(d - \frac{ah}{g})$$

 

[lizzyb]

do i need to have the 'bar' of which to calculate the torque go through the center of mass? as in, from F, draw diagonally toward the top-left of the cart? or can I just draw it straight across?

 

[lizzyb]

how did they put 'a' in the equation for F_y? In all the answer's I can choose from, 'a' (acceleration) is in all of them.hmmm

 

[OlderDan]

so it would be:
$$\sum \tau = w(L - d) - n L = 0$$

So,
$$F_y = w - n = w - \frac{w(L - d)}{L} = \frac{L w - w(L - d)}{L} = \frac{w(L - L + d)}{L} = \frac{wd}{L}$$

hmm, the answers to choose from are things like $$F_y = \frac{W}{2L}(d - \frac{ah}{g})$$

I took a wrong turn earlier. You need to calculate the torque about the center of mass and set that to zero. The F has two components. The horizontal component is the only thing that will accelerate the trailer, and the distance from the line of that force component to the CM is given. This force is F_x = ma = a*W/g. The y component of the hitch force (the one you are looking for) also has a known distance, and the normal force has a known distance. You can set up an equation that can be solved for N in terms of the other things from this torque. Then use the other equation for N from the sum of the vertical forces being zero. Set those two expression for N equal and solve for F_y

 

[lizzyb]

when i calculate the torque, do i use a horizontal 'beam' thing?

$$\sum \tau = nd ...$$

since F goes up to the right I'm not sure how to include it.

edited:
$$\sum \tau = -nd + F(L - d) = 0$$
??

 

[OlderDan]

when i calculate the torque, do i use a horizontal 'beam' thing?

$$\sum \tau = nd ...$$

since F goes up to the right I'm not sure how to include it.

edited:
$$\sum \tau = -nd + F(L - d) = 0$$
??

(L - d) is the correct distance for the vertical component of F. The horizontal component is a perpendicular distance of h from the CM and don't forget the horizontal component is the only force accelerating the trailer.

 

[lizzyb]

this?
$$\sum \tau = F_y(L - d) - F_x h - nd = 0$$
$$\sum F_x = ma = a \frac{W}{g}$$
$$\sum F_y = n + F_y - W = 0$$
??

 

[lizzyb]

ok great! for some reason my sign was different than the answers provided but mine was close enough that i tried it. thanks a lot Dan! this question has two more parts but hopefully with this equation i should be able to figure it out! :-)

 

[lizzyb]

i did it! thanks everyone! i finished my physics homework - 3 hours to spare (and class in 7 hours :-O {but it's chemistry}). you're an answer to my prayers! yay ! i understand it better, too - i now realize that we're to take the torque around a POINT - not a bar. :-)! good night! thanks again!

 

[OlderDan]

this?
$$\sum \tau = F_y(L - d) - F_x h - nd = 0$$
$$\sum F_x = ma = a \frac{W}{g}$$
$$\sum F_y = n + F_y - W = 0$$
??

I think your sign problem is here. The two torques from F are both counterclockwise.

$$\sum \tau = F_y(L - d) + F_x h - nd = 0$$