Right. If you short a resistor, the voltage across the resistor will be zero, so according to Ohm's law, the current through it will be zero.
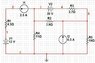
Let's go back to your original question about shorting/removing a current source. I thought of a simple example of showing if you remove the current source, you'll get the wrong answer: Consider a current source I in parallel with a resistor R, and say you want to find its Thevenin equivalent (which, as you should know, is a voltage source V=IR in series with a resistor R). The Thevenin resistance is the ratio of the open-circuit voltage Voc and short-circuit current Isc. The open-circuit voltage will just be Voc=IR. Now, if you say you can remove the current source because you're shorting it out, you'd then be left with just the resistor R connected to the short. The short-circuit current would therefore be Isc=0, and the Thevenin resistance would be infinite. Clearly, that's not correct.
The correct analysis is: When you short the nodes, you can remove the resistor, and all the current from the source will flow through the short, i.e. Isc=I. The Thevenin resistance will therefore be Voc/Isc=IR/I=R. The Thevenin equivalent will consist of a voltage source Voc=IR in series with resistance R, as you'd expect.