- #1
Juntao
- 45
- 0
You got to see the picture 1st.
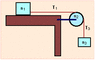
A block of mass m1 = 2 kg rests on a table with which it has a coefficient of friction µ = 0.66. A string attached to the block passes over a pulley to a block of mass m3 = 4 kg. The pulley is a uniform disk of mass m2 = 0.5 kg and radius 15 cm. As the mass m3 falls, the string does not slip on the pulley.
--------
a) With what acceleration does the mass m3 fall?
b) What is the tension in the horizontal string, T1?
c) What is the tension in the vertical string, T3?
=======================
Okay, shouldn't be that HARD of a problem. But this is what I've done so far.
mass 1 (right is positive)
-------
Summation of forces in x direction
T1-u*m1*g=m1a
Summation of forces in y direction
N-m1g=0
N=m1g
mass 3 (up is positive)
------
Summation of forces in y direction
T3-m3*g=m3*a
My biggest question is the following equation correct:
mass 2
------
(T1-T3)R=I*alpha
simplifies to
(T1-T3)R=.5*m2*R^2*(a/R)
or
(T1-T3)=.5*m2*a => is this right for mass 2 for net torque
From here I manipulated the equations until I got a=...
This is what I have so far, but I'm not getting the acceleration value right, unless I made an algebra error.
But the equations look right so far, right?
A block of mass m1 = 2 kg rests on a table with which it has a coefficient of friction µ = 0.66. A string attached to the block passes over a pulley to a block of mass m3 = 4 kg. The pulley is a uniform disk of mass m2 = 0.5 kg and radius 15 cm. As the mass m3 falls, the string does not slip on the pulley.
--------
a) With what acceleration does the mass m3 fall?
b) What is the tension in the horizontal string, T1?
c) What is the tension in the vertical string, T3?
=======================
Okay, shouldn't be that HARD of a problem. But this is what I've done so far.
mass 1 (right is positive)
-------
Summation of forces in x direction
T1-u*m1*g=m1a
Summation of forces in y direction
N-m1g=0
N=m1g
mass 3 (up is positive)
------
Summation of forces in y direction
T3-m3*g=m3*a
My biggest question is the following equation correct:
mass 2
------
(T1-T3)R=I*alpha
simplifies to
(T1-T3)R=.5*m2*R^2*(a/R)
or
(T1-T3)=.5*m2*a => is this right for mass 2 for net torque
From here I manipulated the equations until I got a=...
This is what I have so far, but I'm not getting the acceleration value right, unless I made an algebra error.
But the equations look right so far, right?