pobro44
- 11
- 0
- Homework Statement
- I want to program a two body problem and wish to calculate velocities of bodies when relative velocity is known. Please let me know whether my derivation makes sense.
- Relevant Equations
- Angular momentum of system body acted upon with central force
When only force acting on body is a central force, angular momentum is constant and given by:
L = mr^2 * w
where r is distance from origin, and w is angular velocity.
Angular momentum can also be written as following:
L = r x mv = rmv * sin(theta) where v is tangential velocity, which is orbital velocity
so we can equate the two expressions above and
w = v * sin(theta) / r
since angular velocities of two bodies are the same, we can write
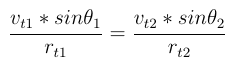 where t1 stands for first body, and t2 for second
where t1 stands for first body, and t2 for second
I suppose that angles that position vectors make with velocity vector are the same, so sines are equal and
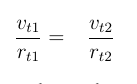
if we define relative velocity between two bodies as
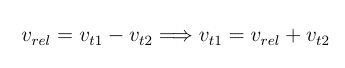
and plug that back into previous equation we get orbital velocities of each body from their relative velocity at that point
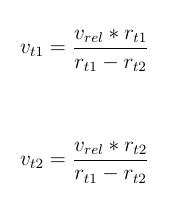
Is this correct? I derived it by myself so any feedback would be appreciated :)
L = mr^2 * w
where r is distance from origin, and w is angular velocity.
Angular momentum can also be written as following:
L = r x mv = rmv * sin(theta) where v is tangential velocity, which is orbital velocity
so we can equate the two expressions above and
w = v * sin(theta) / r
since angular velocities of two bodies are the same, we can write
I suppose that angles that position vectors make with velocity vector are the same, so sines are equal and
if we define relative velocity between two bodies as
and plug that back into previous equation we get orbital velocities of each body from their relative velocity at that point
Is this correct? I derived it by myself so any feedback would be appreciated :)
Last edited: