Matt Raj
- 6
- 0
- Homework Statement
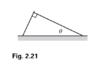
- One stick leans on another as shown in Fig. 2.21. A right angle is formed where they meet, and the right stick makes an angle θ with the horizontal. The left stick extends infinitesimally beyond the end of the right stick. The coefficient of friction between the two sticks is μ. The sticks have the same mass density per unit length and are both hinged at the ground. What is the minimum angle θ for which the sticks don’t fall? (From Introduction to Classical Mechanics by David Morin)
- Relevant Equations
- N = (Mg/2) sin θ
F_f = (mg/2)cosθ
I attempted this problem trying to balance torques but I couldn't because the length of the left stick is unknown. From the right stick I got that mg/2* cos θ = F_f but from the left stick I got that Mg/2sin θ =N* r where r is the ratio of the length of where the sticks meet and the total length of the left stick. I looked at the answer and it didn't involve any ratio as such; in fact, the equation from the left stick provided in the solution was N = (Mg/2) sin θ. I'm confused why the solution didn't incorporate the length of the stick for the normal force on the left stick. Besides that one equation, I can solve the rest of the problem.
Update: I solved the problem by finding r but I'd like to know how the book found the equation " N = (Mg/2) sin θ " whereas I got N*cot θ* l/L = Mgsin θ and had to do some extra work.
Update: I solved the problem by finding r but I'd like to know how the book found the equation " N = (Mg/2) sin θ " whereas I got N*cot θ* l/L = Mgsin θ and had to do some extra work.
Attachments
Last edited: