You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Two Pulley Problem: Solve & Find Correct Answer
- Thread starter ietr
- Start date
-
- Tags
- Pulley pulley problem
AI Thread Summary
The discussion centers on solving a physics problem involving two pulleys and three blocks with different weights. Participants analyze the forces acting on each block, applying Newton's second law to derive equations for their accelerations and tensions. A key point raised is the assumption that tension remains constant throughout the string, which is challenged as there may be two separate strings involved. The confusion arises when trying to equate the accelerations of the blocks, leading to contradictory results. Ultimately, the importance of understanding the system's configuration and the implications of tension differences is emphasized for accurately solving the problem.
Physics news on Phys.org
ietr
- 4
- 0
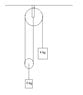
The question is to find the accelerations of the two blocks
- 22,802
- 14,854
Why don't you show us what you tried and what your result was and we can point you in the correct direction? It will be much more instructive.
ietr
- 4
- 0
Okay. I got that question now, but this one is really troubling me. This is what I've tried sofar:
First I draw FBD for each of the blocks. Applying F = MA for each block:
500 g block
----------------
500 g = 1/2 kg
The string attached to it has a tension T.
let it have an acceleration a1 downward: 1/2g - T = 1/2 (a1)
100 g block
----------------
100 g = 1/10 kg
taking the components, we have gsin(30) along the string and gcos(30) canceled by normal reaction.
Let it have an acceleration of a2 downward on the incline then
F = MA
(1/10) g sin(30) - T = (1/10) a2
50 g block
---------------
50 g = 50/1000 = 1/20 kg
let it have an acceleration a3 downward then
(1/20) g - T = (1/20) a3
Obviously there is some error in the above three equations because there are four unknowns: T, a1, a2 and a3.
I'm having trouble understanding this:
* Will the tension remain T along all segments of the string, unlike what I have assumed above?
* Since the string length is constant, the accelerations a1, a2 and a3 must be equal but if we set them all equal to 'a', then we have only two unknowns T and 'a' and three equations, and further on solving them we do not get the correct answer.
First I draw FBD for each of the blocks. Applying F = MA for each block:
500 g block
----------------
500 g = 1/2 kg
The string attached to it has a tension T.
let it have an acceleration a1 downward: 1/2g - T = 1/2 (a1)
100 g block
----------------
100 g = 1/10 kg
taking the components, we have gsin(30) along the string and gcos(30) canceled by normal reaction.
Let it have an acceleration of a2 downward on the incline then
F = MA
(1/10) g sin(30) - T = (1/10) a2
50 g block
---------------
50 g = 50/1000 = 1/20 kg
let it have an acceleration a3 downward then
(1/20) g - T = (1/20) a3
Obviously there is some error in the above three equations because there are four unknowns: T, a1, a2 and a3.
I'm having trouble understanding this:
* Will the tension remain T along all segments of the string, unlike what I have assumed above?
* Since the string length is constant, the accelerations a1, a2 and a3 must be equal but if we set them all equal to 'a', then we have only two unknowns T and 'a' and three equations, and further on solving them we do not get the correct answer.
Attachments
- 22,802
- 14,854
ietr said:Obviously there is some error in the above three equations because there are four unknowns: T, a1, a2 and a3.
I'm having trouble understanding this:
* Will the tension remain T along all segments of the string, unlike what I have assumed above?
If instead of being inclined by 30 degrees, the thread would be hanging vertically with a 100 g weight in the middle, would the tension be the same above and below the weight?
* Since the string length is constant, the accelerations a1, a2 and a3 must be equal but if we set them all equal to 'a', then we have only two unknowns T and 'a' and three equations, and further on solving them we do not get the correct answer.
Yes, the accelerations have to be of equal magnitude - but be very mindful of their direction, if one of the ends accelerates up, the other end accelerates down.
ietr
- 4
- 0
Orodruin said:If instead of being inclined by 30 degrees, the thread would be hanging vertically with a 100 g weight in the middle, would the tension be the same above and below the weight?
I guess that yes the tension would be T in both the sides of the weight
Yes, the accelerations have to be of equal magnitude - but be very mindful of their direction, if one of the ends accelerates up, the other end accelerates down.
if a1 = a2 = a3, and we assume that their directions are:
a1 : of 500 g downwards
a2: of 100 g upwards along the incline
a3: of 50 g upwards
then the equations become (assuming that the tension is T along the length of the string)
(1/2)g - T = (1/2)a
T - (1/10)g sin(30) = (1/10)a
T - (1/20)g = (1/20)a
Solving these equations for 'a', we get a = (3/4)g from the first two equations and a = (9/11)g from the first and third equations. How can there be two values of 'a'?
- 42,640
- 10,429
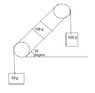
It's not clear from your diagram how the 100g block is attached. Looks to like there are (logically, at least) two separate strings - one runs from the 500g block, over the top pulley, to the 100g block; the second runs from the 100g block, over the lower pulley, to the 50g block. There is no reason why the tensions should be the same in the two sections of string.ietr said:if a1 = a2 = a3, and we assume that their directions are:
a1 : of 500 g downwards
a2: of 100 g upwards along the incline
a3: of 50 g upwards
then the equations become (assuming that the tension is T along the length of the string)
(1/2)g - T = (1/2)a
T - (1/10)g sin(30) = (1/10)a
T - (1/20)g = (1/20)a
Solving these equations for 'a', we get a = (3/4)g from the first two equations and a = (9/11)g from the first and third equations. How can there be two values of 'a'?
- 22,802
- 14,854
haruspex said:It's not clear from your diagram how the 100g block is attached. Looks to like there are (logically, at least) two separate strings - one runs from the 500g block, over the top pulley, to the 100g block; the second runs from the 100g block, over the lower pulley, to the 50g block. There is no reason why the tensions should be the same in the two sections of string.
It does not matter much how it is attached. What matters is that it is attached (and parallel to the inlined plane).
ietr: You should also try to think a bit more about what happens for the weight on the inclined plane. What forces from the threads are acting upon it?
Also, think a bit what happens if you are in a tug of war contest. If the guy on your team who is in front of you happens to be so strong that he easily defeats the other team by himself, what is the rope tension you need to provide to the rope between you to win? What is the rope tension between him and the opposing team?
- 42,640
- 10,429
No, it does matter. Within the range of possibilities in the diagram, the 100g block would tip over, even if there is no friction.Orodruin said:It does not matter much how it is attached. What matters is that it is attached (and parallel to the inlined plane).
But as I posted, ietr's error is in taking the tension as the same throughout. There are effectively two separate strings.
Similar threads
- Replies
- 10
- Views
- 1K
- Replies
- 15
- Views
- 1K
- Replies
- 2
- Views
- 2K
- Replies
- 15
- Views
- 5K
- Replies
- 18
- Views
- 1K
- Replies
- 12
- Views
- 1K
- Replies
- 24
- Views
- 3K
- Replies
- 22
- Views
- 303
- Replies
- 24
- Views
- 2K
- Replies
- 13
- Views
- 1K
Hot Threads
-
The problem of one tube and two balls on a plane
- Started by crazy lee
- Replies: 60
- Introductory Physics Homework Help
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math