schniefen
- 177
- 4
- Homework Statement
- This regards section 10.3.1 in Griffith’s Introduction to electrodynamics, specifically the proof for why an extra factor is added when integrating the charge density when it depends on the retarded time.
- Relevant Equations
- Average speed: ##\frac{x_f-x_i}{t_f-t_i}##
In Griffith’s section 10.3.1, when proving why there is an extra factor in integrating over the charge density when it depends on the retarded time, he makes the argument that there can only ever be one point along the trajectory of the particle that “communicates” with the field point. Because if there were two such points, the component of the particles velocity towards ##\mathbf r## would be greater than the speed of light ##c##.
I don’t follow the geometric argument for this. How can one determine the velocity of the particle in a given direction?
The argument is that ##\mathscr{r}_1-\mathscr{r}_2 =c(t_2-t_1)## (where ##\mathscr{r}## is the magnitude of a scripted r). ##\mathbf{w}(t_r)## is the position of the particle at the retarded time. The times ##t_2,t_1## is the time it takes the light to travel the distances to ##\mathbf r##. How is this related to the average speed of the particle?
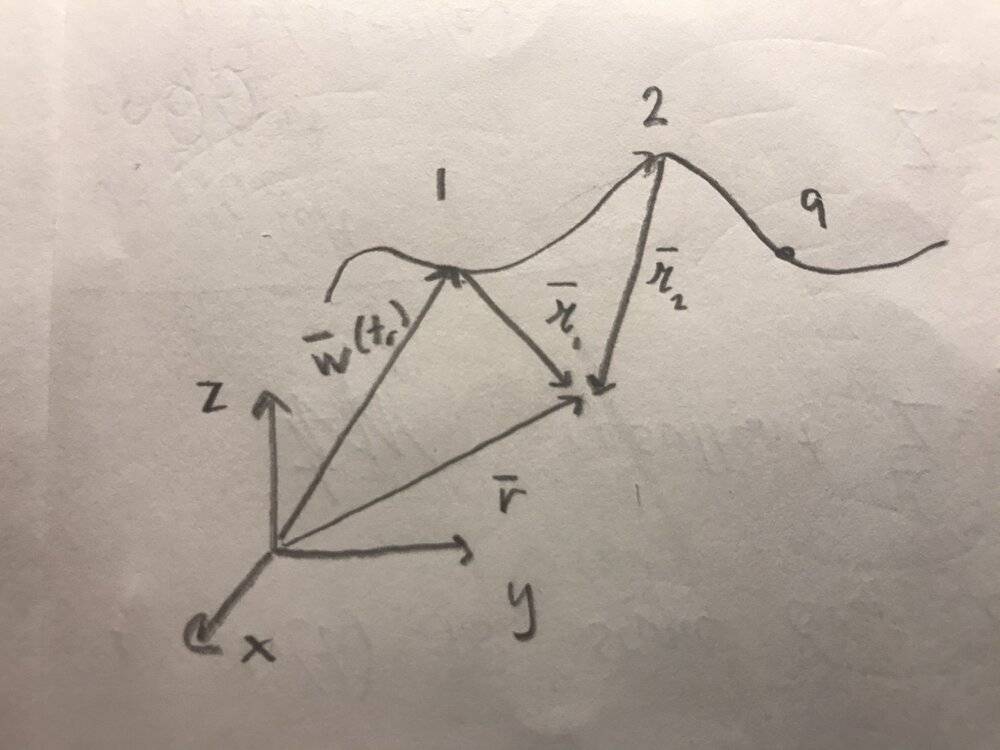
I don’t follow the geometric argument for this. How can one determine the velocity of the particle in a given direction?
The argument is that ##\mathscr{r}_1-\mathscr{r}_2 =c(t_2-t_1)## (where ##\mathscr{r}## is the magnitude of a scripted r). ##\mathbf{w}(t_r)## is the position of the particle at the retarded time. The times ##t_2,t_1## is the time it takes the light to travel the distances to ##\mathbf r##. How is this related to the average speed of the particle?
Last edited: