Understanding RC Capacitor Discharge Theory

[mathg33k]

Homework Statement

This is not a true homework problem but rather my interpretation of RC Capacitor theory. What is the action of a capacitor in RC first-order circuits?

Homework Equations

The Attempt at a Solution

From what i understand, when a capacitor is being charged, charges move from the '-' plate to the '+' plate. Then when discharged, charges move back from the '+' plate back to the '-' plate and thus create current flow in the opposite direction. Thus, current flows in the opposite direction.

Why is this appear contradictory to the derivation from my textbook of RC circuit discharge?
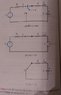
1. The current direction does not reverse in the first photo with the circuit diagram.

2. Also, if the current direction is reversed, I find that V/R = C dv/dt, or dv/dt - (1/RC)v = 0 which I know to be wrong. This corresponding KCL equation no longer matches the derivation in the second picture leading to dv/dt + (1/RC)v = 0. I believe the textbook's equation is correct because I've seen it both online and in other textbooks.
Is this an issue with passive sign convention that I am not understanding?

 

[Simon Bridge]

I cannot see the context for the first pic - it looks like the arrow on the current is just indicating the direction taken to be "positive" - so when the capacitor discharges, the value of i is negative.

For the second pic:
The textbook has a definition of current - $$i=C\frac{dv}{dt}$$...
When the capacitor is discharging, the sign of dv/dt changes.
Please show your working and reasoning step by step.

 

[mathg33k]

Thanks for your post Simon. I didn't consider that the sign simply changed and the diagram was pointing in a reference direction. I managed to reason through it myself, here's how.

Say that the capacitor was charged up to 6V and the resistor has a value of 2 ohms. At t(0-), the current through the resistor is 3A. Then, the current going out of the top of the capacitor is also 3A, which agrees with the theory of charge flowing back from the positive terminal.

Using the provided definition once the capacitor discharges, then a node equation written at the positive terminal of the capacitor as shown would be
V/R + C dv/dt = 0.

V/R, if we use
So, C dv/dt = -2.

I mixed up dv/dt with di/dt because I was thinking that dv/dt could never change sign. But dv/dt actually does go negative because the voltage in the capacitor begins to decrease (which should be obvious but for some reason I missed it.) Thanks!

 

[Simon Bridge]

No worries - enjoy.