Understanding the Physics of a Cylinder Rolling Down a Slope

[TauMuon]

I would appreciate some help on this question involving a cylinder rolling down a slope; I'm far from comfortable with the physics involved.

Question here:

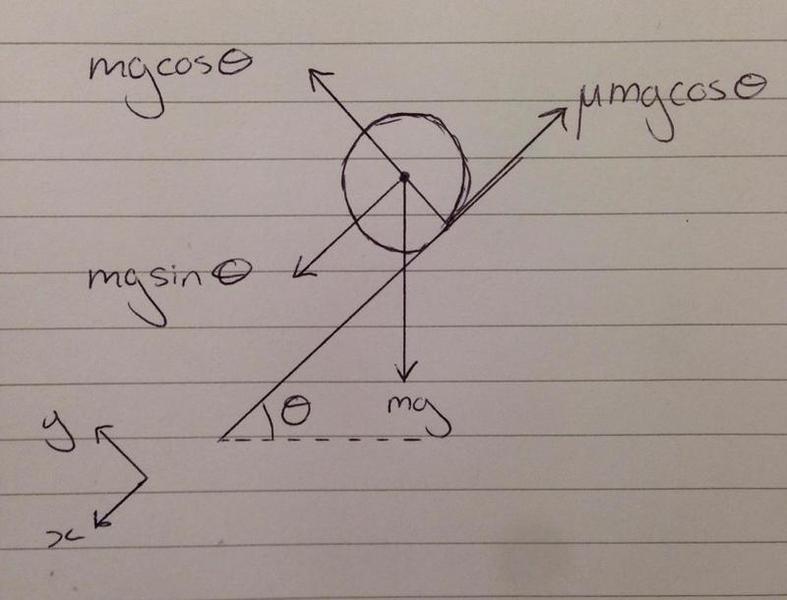
This is my free-body diagram of the forces acting on the cylinder:

Expressions for the acceleration in the x- and y-directions in terms of the forces acting on the cylinder:

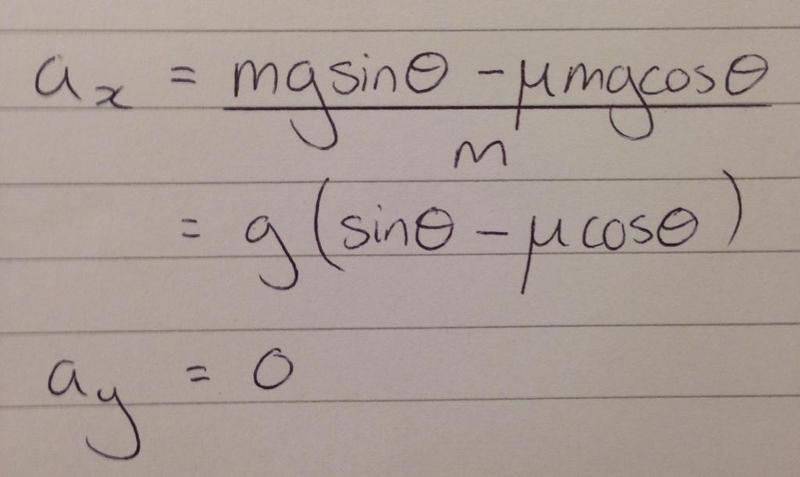
Now I think the above is okay. The following is where I get a bit lost...

Expression for the angular acceleration:

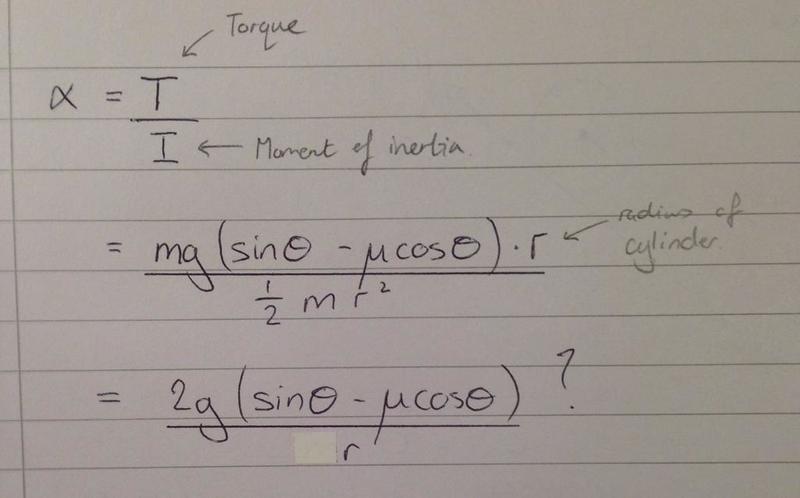
Acceleration along x (didn't it already ask for this..?) :

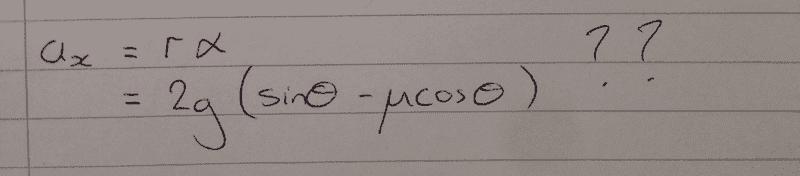
I really have no clue if the above is even remotely correct. I'm very fuzzy on the physics at the moment, so if someone could take the time to explain it to me I would be immensely grateful.

Thanks!

 

[BvU]

RE diagram: it's a bit strange that $m\vec g\cos\theta$ is pointing upwards. After all, the vectors $m \vec g\cos\theta$ and $m \vec g\sin\theta$ should add up to $m\vec g$

An unexplained ( :) ) $\mu$ pops up in the diagram.

If I take the diagram seriously, the cylinder should take off from the ramp in the vertical y-direction: forces don't add up to 0 (see first comment re diagram)

so much for a) and b).

c) there's $\mu$ again. For the friction force we usually write $|\vec F_{fric, max}| = \mu |\vec F_N|$ where $\vec F_N$ is the normal force. Hence my "confusion": the friction force let's the thing rotate, but perhaps the maximum friction force is more than is needed to satisfy the no-slip condition... So you want to wonder about this non-slipping and what it means for $\alpha$ and thereby for the friction force..