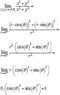Use polar coordinates to find the limit
- Thread starter Faka
- Start date
Click For Summary
Homework Help Overview
The discussion revolves around using polar coordinates to evaluate a limit as the point approaches the origin in the Cartesian plane. The original poster presents an exercise that involves understanding the behavior of a function in polar coordinates.
Discussion Character
- Exploratory, Conceptual clarification
Approaches and Questions Raised
- Participants are discussing the steps taken so far and questioning how to determine the limit. There is a mention of the nature of continuous functions and their limits, prompting further inquiry into the original poster's understanding.
Discussion Status
The conversation is ongoing, with participants seeking clarification on the original poster's approach and exploring the concept of limits in the context of continuous functions. Some guidance has been offered regarding the nature of limits, but no consensus has been reached.
Contextual Notes
The original poster has not provided specific details about the function in question, which may affect the discussion. There is an emphasis on the transition to polar coordinates and the implications of approaching the origin.
Similar threads
- · Replies 19 ·
- · Replies 14 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 24 ·
- · Replies 3 ·
- · Replies 3 ·