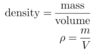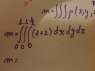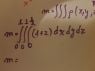The attempt that you posted is too small and I cannot click on it to get a better view. But from what I can see, I suggest the following.
1. Understand, from the ranges of x, y and z given by you, the shape of the region you are interested in. In other words, answer the first question and sketch the region. In your graph, you only showed a few isolated points. You did not sketch the region in space.
2. The relevant equation posted by you is not adequate. Density = mass / volume is good only if the density is constant. In your case, the density depends on position (your equation: ρ = 1 + z). Then you must use the differential form:
dm = ρ dV,
and integrate this to get the total mass. It will be a triple integral.