Sagrebella
- 61
- 2
Hello,
Could someone please check my answer to this problem involving vectors. I have a feeling my answers are totally off; especially for B and C. All my work and applicable equations are shown in the pictures below. If my answer is wrong, please provide me with guidelines for solving the problem. I'm not expecting anyone to just give me the answer :)
Thanks!
Problem 8
You are in your kayak, paddling across the Charles River, which we can treat as having parallel banks separated by a distance of 480. m. The river is flowing east at a constant speed of 1.40 km/h, and you paddle your kayak at a constant velocity, relative to the water, of 5.20 km/h at an angle of 15.0° east of north.
(a) What is your velocity relative to a fixed point on the shore? Your velocity relative to the shore is: _________ km/h, at an angle of __________° east of north.
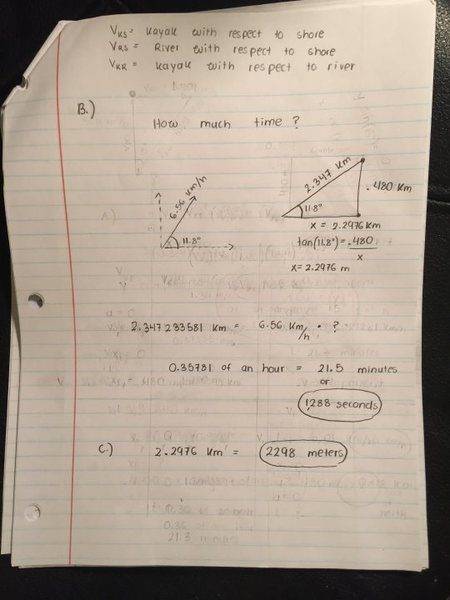
(b) How much time, in seconds, does it take you to paddle from one bank of the river to the other, under the conditions described above? Note that you will not land on the far side at the point directly across the river from where you started.
(c) While you are crossing the river, how far downriver do you travel (in meters)?
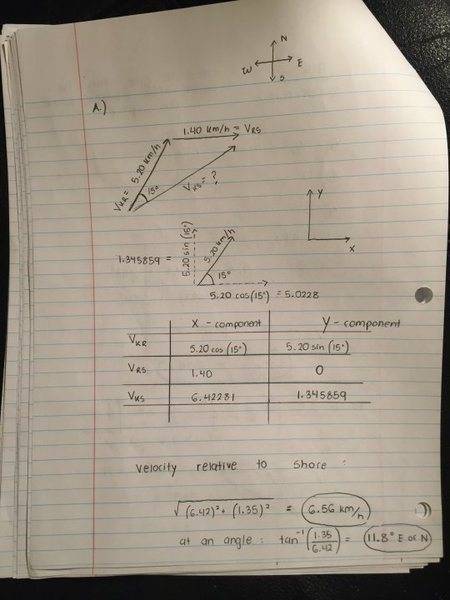
Could someone please check my answer to this problem involving vectors. I have a feeling my answers are totally off; especially for B and C. All my work and applicable equations are shown in the pictures below. If my answer is wrong, please provide me with guidelines for solving the problem. I'm not expecting anyone to just give me the answer :)
Thanks!
Problem 8
You are in your kayak, paddling across the Charles River, which we can treat as having parallel banks separated by a distance of 480. m. The river is flowing east at a constant speed of 1.40 km/h, and you paddle your kayak at a constant velocity, relative to the water, of 5.20 km/h at an angle of 15.0° east of north.
(a) What is your velocity relative to a fixed point on the shore? Your velocity relative to the shore is: _________ km/h, at an angle of __________° east of north.
(b) How much time, in seconds, does it take you to paddle from one bank of the river to the other, under the conditions described above? Note that you will not land on the far side at the point directly across the river from where you started.
(c) While you are crossing the river, how far downriver do you travel (in meters)?
Last edited: