doggydan42
- 169
- 18
Homework Statement
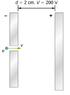
An electron enters a region between two large parallel plates made of aluminum separated by a distance of 2.0 cm and kept at a potential difference of 200 V. The electron enters through a small hole in the negative plate and moves toward the positive plate. At the time the electron is near the negative plate, its speed is Assume the electric field between the plates to be uniform, and find the speed of electron at (a) 0.10 cm, (b) 0.50 cm, (c) 1.0 cm, and (d) 1.5 cm from the negative plate, and (e) immediately before it hits the positive plate
2. Homework Equations
If V is the potential difference and K is the kinetic energy, then
$$-q\Delta V = \Delta K = \frac{1}{2} m(v^2-v_0^2)
\\\Delta V = \int_{a}^b \vec E \bullet d{\vec l}$$
The Attempt at a Solution
To solve, I used the first formula. q is the charge of an electron, ##\Delta V## is given, and m would be the mass of an electron. Though my problem is that this means that the velocity does not depend on the distance from the plate.
Thank you in advance
Attachments
Last edited: