Avalanche
- 23
- 0
Homework Statement
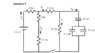
Please look at the attachment for the circuit.
The question is this:
The switch has been closed for a long time. It is then opened. How long does it take for the potential across the 4μF capacitor to fall to half of its initial value?
Homework Equations
V = V0e^(-t/RC)
The Attempt at a Solution
Once the switch is opened, the capacitor would begin to discharge creating a potential difference. The equation I tried to solve is
0.5 = e^(-t/(4.0*R))
The problem I'm having is that I don't know what R, the equivalent resistance is for this circuit.
The answer is that it takes 10.2 μs for the potential to drop to half of its initial value. Working backwards, I get the equivalent resistance is 3.68 ∏. How do I get that?