Volume of a segment of a sphere

[icesalmon]

Homework Statement

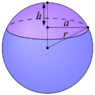
Let a sphere of radius r be cut by a plane, thereby forming a segment of height h. Show that the volume of this segment is (∏h²(3r-h))/3

Homework Equations

V_sphere = (4∏r³)/3
Ax + By + C = 0
not sure if these are helpful at all.

The Attempt at a Solution

I don't know how to start, I don't know what segment they are referring to when the book says "this" segment? I wrote down, for relevant equations, what I think is the 2 dimensionsal plane equation, should I have used one for the x-y-z plane instead since the volume of revolution exists in 3-dimensions? I also don't really know if (4pir³)/3 is going to help at all, I'm putting down things I feel may help in some way. I think I should use the plane that intersects the sphere as part of the equation for my radius, but I am not sure about the plane equation I have down so I am nervous about continuing. Thanks

 

[SteamKing]

Imagine you have a sphere with the center at the origin.

Take a plane which is parallel to the x-y plane but located h units below the 'north pole' of the sphere, where the 'north pole' has coordinates (0,0,R). The plane and the z-axis therefore intersect at (0,0,h).

What is the volume of the spherical cap lying above z = h all the way to z = R?

A picture could always come in handy.

 

[icesalmon]

x² + y² + z² - h? Maybe my picture is wrong, I have it drawn so that the yz plane is parallel to my paper and the x-axis is coming off of my page so the plane of intersection is parallel to the x-y plane.

This is related to a volume of revolution from Calculus II, it is not a problem from Calculus III. I wasn't clear about that, my mistake.

 

[icesalmon]

In order the find the volume I have to have bounds, and I'm completely lost here. My bounds are from x = h+A -> y = h+B, I found these by setting my plane equation equal to the equation for my sphere centered at the origin. For my height I have x2 + y2 + z2 - h so I multiply them and integrate and I get 2pi((h+A)⁴)/4 + ((h+B)²(h+A)²)/2 + (z²(h+A)²)/2 -(h(h+A)²)/2)

 

[Sourabh N]

The integration (whose bounds you are speaking of, presumably) would be considerably simpler if done in spherical polar coordinates.

 

[icesalmon]

fair enough, except I'm not supposed to use them. or double or triple integrals for that matter, this is a shell method/disk/washer method problem from Calculus II.

 

[Sourabh N]

I'm not sure what is part of Calculus II (Non-US bachelors, sorry). But in any case, if using Cartesian coordinates, having your origin at the top of the spherical cap (the north pole of the sphere) gives the bounds as x = 0 to r, y = 0 to r and z = 0 to -h, with the constraint that x² + y² + z² <= r². Does that simplify things?

 

[icesalmon]

I'm still not sure if my height, x2 + y2 + z2 -h, or my radius x, are correct. I need to use shell method for this volume. I am not seeing how the constraint helps. And I need limits of integration for one variable, you have three there. Also I'm not seeing that the plane intersects the sphere so that it cuts out a distance of "r" units on the x-axis. If the plane is above the x-axis, how can it be r units long?

 

[SteamKing]

The surface of the sphere is defined by the equation:

x^2 + y^2 + z^2 = R^2

A plane parallel to the x-y axis which intersects the z axis at the point (0,0,h) will create an intersection with the spherical surface which is circular in shape. The radius of this circle will be sqrt(R^2 - h^2).

 

[icesalmon]

I believe I understand everything you've said there, except for the final part. How did you get sqrt(R² - h²) for the radius?
I understand that, while using shell method to calculate the volume of this segment, that (r-h) gives the area of the radius of some arbitrary shell, but why are these quantities squared in the radius?

 

[haruspex]

SteamKing is measuring h from the centre of the sphere. Substitute R-h if you want to measure from the surface, as in the OP. Or use z generically and integrate wrt z from R-h to R.

 

[icesalmon]

okay, so I believe I used z generically and for my integrand I have z*sqrt(r^2-x^2-y^2)dz where z ranges from r-h -> r. After integrating and simplification I have pi*sqrt(r^2-x^2-y^2)(2rh - h^2) the answer in the back of the book just says "proof".

 

[SteamKing]

I don't understand your answer. After integrating and applying limits of integration, x and y should disappear. You should show your work in more detail.

 

[icesalmon]

for my height I have r-h but if i integrate wrt z I have to have z as a function of x,y so I re-write the sphere equation so that z = sqrt(r^2-x^2-y^2). I don't know why I had z in my original integrand, the height I think is (r-h). (r-h)sqrt(r^2-x^2-y^2) I treat as a constant since it doesn't have any terms including z so I pull it out in front of the integral and integrate 1dz which becomes 2pi(r-h)sqrt(r^2-x^2-y^2)z and I evaluate that at (r-h) and r to get 2pi(r-h)*sqrt(r^2-x^2-y^2)(r)-2pi(r-h)²sqrt(r^2-x^2-y^2)

 

[haruspex]

for my height I have r-h but if i integrate wrt z I have to have z as a function of x,y so I re-write the sphere equation so that z = sqrt(r^2-x^2-y^2).

That gives you the value of z for a given x and y for a point on the surface of the sphere. Not much use here.
First decide how you are going to carve the segment into elements.
I would choose a washer structure: for a given z, R-h < z < R, there is a disc at distance z from the centre of the sphere, thickness dz. What is its area?
Or with the shell approach you could carve it into concentric cylinders (of varying lengths) centred on the z axis. In this case, a given cylinder has radius r = sqrt(x^2+y^2) and thickness dr. You need to figure out the range for z in terms of r.

 

[icesalmon]

does z range from r-h to r or is it just h to r?
sorry this is really hard for me to picture on my drawing

 

[haruspex]

If you centre the sphere at the origin then z ranges from r-h to r.

 

[icesalmon]

I'm completely lost. If that distance isn't correct, than I feel I have to account for some distance the sphere's south pole has been raised off of the origin. If I call that distance "d" than for the height of the segment I would have to first subtract off that distance "d" to get back to the south pole of the sphere and then subtract away "h" if I'm understanding that "h" is how high up on the diameter of the sphere the plane is.

 

[SteamKing]

I got my reference for h mixed up earlier.

The attached picture shows the spherical cap:

 

[icesalmon]

thanks a lot for the picture, i'll try to understand this again.
edit: I'm still thinking it goes from (r-h), the lower bound, to r at the north pole of the sphere. But "r" starts outside of the region! :(

 

[haruspex]

thanks a lot for the picture, i'll try to understand this again.
edit: I'm still thinking it goes from (r-h), the lower bound, to r at the north pole of the sphere.

That's what SteamKing's picture shows. Measuring z up from the centre of the sphere, z runs from r-h (the lower end of the arrow labelled h) to r (the top end of that arrow).

But "r" starts outside of the region! :(

I don't know what you mean. r is the radius of the sphere. Where does it 'start'? Do you mean the origin?

 

[icesalmon]

yeah, it lies outside of that purple region. It seems just as useful to have 2r-h for that distance. I'm just measuring back to the start of the purple area anyways.