pixelized
- 7
- 0
I solved for 2 correctly but I can't figure out what to do for #3 Any help would be much appreciated. I think it might involve L = r x p , but I'm not entirely sure.
2. [1pt]
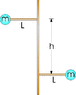
Two lightweight rods L = 20.5 cm in length are mounted perpendicular to a vertical axle and at 180° to each other (see figure below).
At the end of each rod is a m = 602 g mass. The rods are spaced h = 35.7 cm apart along the axle. The axle rotates at 28.7 rad/s such that the angular velocity vector points upward (+). What is the component of the total angular momentum along the axle?
3. What angle does the vector angular momentum make with the axle?
2. [1pt]
Two lightweight rods L = 20.5 cm in length are mounted perpendicular to a vertical axle and at 180° to each other (see figure below).
At the end of each rod is a m = 602 g mass. The rods are spaced h = 35.7 cm apart along the axle. The axle rotates at 28.7 rad/s such that the angular velocity vector points upward (+). What is the component of the total angular momentum along the axle?
3. What angle does the vector angular momentum make with the axle?