hangingwire
- 8
- 0
Homework Statement
Find cord tension and force on the hinge on this beam given the following:
Picture of the equation (in attachments)
beam is 10 kg
beam is 8.0m long
Homework Equations
[T=0
[F=0
[h2]The Attempt at a Solution[/h2]
Finding the Torque on the wire...
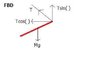
I attached my FBD I drew. Before I start, one question? Since the beam is on an angle, would there be a horizontal force on the x-axis resulting from the Mass of the beam? If so, It could be 60 degrees? Mg Sin60?
That is my attempt using the "Z-rule" in angles
Anyways:
[T= 0
Tcw = Tccw
mg(d) = Tsin( ) * (d)
(10)(9.8)(4) = T sin30 * (8m) ----> Sin 30* given that directly across is 90 degrees + 60 degrees given = 30 degrees left at where the beam and wire are attached.
392N = T sin30 * (8m)
392N divided by 8m = 49
49 = T sin30
49 divided by sin30 --> 98?
The answer is 49N. Why did I get double the answer? Is there something with my angles?