jaus tail
- 613
- 48
Homework Statement
Homework Equations
Substitution.
The Attempt at a Solution
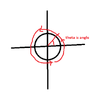
Since the circle is of unit radius and around origin,
limits are x = -1 to 1, and y = -1 to 1
I replaced x by cos t, and y by sin t.
But what to put in place of ds?
I thought about divergence theorem, but then I'd have to find curl of F.
How to break ds in terms of dx + dy or dt?