Stephanus
- 1,316
- 104
Dear PF Forum
I want to know about these questions that are still bothering me,
Does the universe have preferred frame of refference?
Why there's twins paradox?
Motion is relative, why 1 clock experiences time dilation while the other doesn't?
V = \sqrt\frac{3}{4} ≈ 86.6\%
If V define ratio of speed of light, then Lorentz factor is 2.
There are 4 probes.
Clocks are synchronized and reset. Time = T0
Their distance is 100 lys according to Pic 01
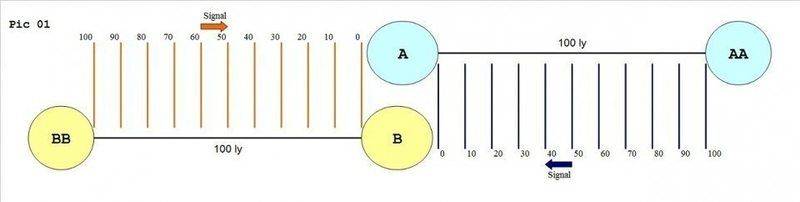
It's been 100 years since the clocks are synchronized and reset.
They have been sending digital signals.
The signals contain respective time and status, the time when they fire their rocket.
Then BB and B, preprogrammed, fire their rockets for 1 second, catapult them for V and stop.
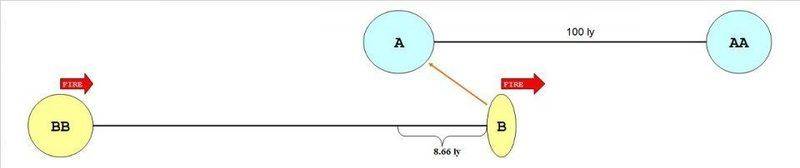
A would have said. "Wow, B is traveling 86.6%c, but BB still stays". Is that right?
Because there's no way that A will know that BB has fired its rocket.
And after 10 years in A clock, will A still consider BB still at rest?
Because A only receives BB time and status, which is the rocket has never been fired, yet.
Does A still see that BB hasn't been contracted yet, and sees that B is already contracted?
Does A read BB clock showing T0+10 years?
And one more thing, tell me if I calculate correctly.
After 10 years in A clock, B keep sending signals
A will read B clock... at
L = V * Tb,
L = Distance traveled by B to send signal so that the signal will be received by A in 10 years.
Ta = L, Time taken by Light to reach A from L
Ta + Tb = 10
L + L/V = 10
L=10V/(1+V)
L = 4.641 Ly
Tb = 5.359 Ly
Lorentz factor is 2, so the clock in B reads 2.6795 years.
Is that right, that in 10 years, A will read the signal that B is T0+102.6795 years?
Back to T100
Would A see Pic03 the instant if rocket B and BB are fired and shot at V?
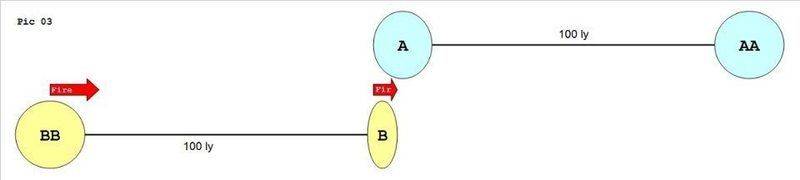
B is contracted while BB isn't, is this the right picture?
What if rocket A (and AA) is fired?
Would A see Pic04 the instant A (and AA) is shot at V?
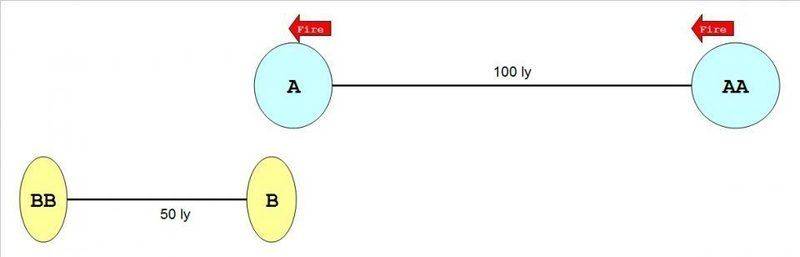
Both BB, B and the distance is contracted by 50%
Does this why twins paradox occur.
Because in both cases the distance between A-AA and B-BB decreases but there is asymmetry?
But I don't ask when B reaches AA or A reaches BB, it's much more complicated I think with length contraction, where BB can reach A before B reach AA. I'll ask once I get this picture.
I want to know about these questions that are still bothering me,
Why there's twins paradox?
Motion is relative, why 1 clock experiences time dilation while the other doesn't?
V = \sqrt\frac{3}{4} ≈ 86.6\%
If V define ratio of speed of light, then Lorentz factor is 2.
There are 4 probes.
Clocks are synchronized and reset. Time = T0
Their distance is 100 lys according to Pic 01
It's been 100 years since the clocks are synchronized and reset.
They have been sending digital signals.
The signals contain respective time and status, the time when they fire their rocket.
Then BB and B, preprogrammed, fire their rockets for 1 second, catapult them for V and stop.
A would have said. "Wow, B is traveling 86.6%c, but BB still stays". Is that right?
Because there's no way that A will know that BB has fired its rocket.
And after 10 years in A clock, will A still consider BB still at rest?
Because A only receives BB time and status, which is the rocket has never been fired, yet.
Does A still see that BB hasn't been contracted yet, and sees that B is already contracted?
Does A read BB clock showing T0+10 years?
And one more thing, tell me if I calculate correctly.
After 10 years in A clock, B keep sending signals
A will read B clock... at
L = V * Tb,
L = Distance traveled by B to send signal so that the signal will be received by A in 10 years.
Ta = L, Time taken by Light to reach A from L
Ta + Tb = 10
L + L/V = 10
L=10V/(1+V)
L = 4.641 Ly
Tb = 5.359 Ly
Lorentz factor is 2, so the clock in B reads 2.6795 years.
Is that right, that in 10 years, A will read the signal that B is T0+102.6795 years?
Back to T100
Would A see Pic03 the instant if rocket B and BB are fired and shot at V?
B is contracted while BB isn't, is this the right picture?
What if rocket A (and AA) is fired?
Would A see Pic04 the instant A (and AA) is shot at V?
Both BB, B and the distance is contracted by 50%
Does this why twins paradox occur.
Because in both cases the distance between A-AA and B-BB decreases but there is asymmetry?
But I don't ask when B reaches AA or A reaches BB, it's much more complicated I think with length contraction, where BB can reach A before B reach AA. I'll ask once I get this picture.


