Patdon10
- 85
- 0
Homework Statement
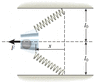
A horizontal slingshot consists of two light, identical springs (with spring constants of 57 N/m) and a light cup that holds a 1-kg stone. Each spring has an equilibrium length l0 = 47 cm. When the springs are in equilibrium, they line up vertically. Suppose that the cup containing the mass is pulled to x = 0.8 m to the left of the vertical and then released.
(a) Determine the system's total mechanical energy.
(b) Determine the speed of the stone at x = 0.
Homework Equations
Potential Elastic Energy: PE = (1/2)kx2
Conservation of energy: 1/2mv2 + (1/2)kx2 = 1/2mv2 + (1/2)kx2
The Attempt at a Solution
This is really tough for me. I'm really not sure how to approach this.
Starting with problem a...
There are two springs and the system is not in motion initially. We know that total mechanic energy is change in K + change in PE.
The equation would be E = (0) + kx2 = (57)(.8) = 45.6 J note I didn't make it (1/2)kx^2 because there are 2 springs.
This is not the correct answer. Any help would be appreciated.