MMS
- 146
- 4
Hello!
I'm pretty much translating this question word by word, so if you have problem understanding something off of it, please, let me know and I'll try explaining it better.
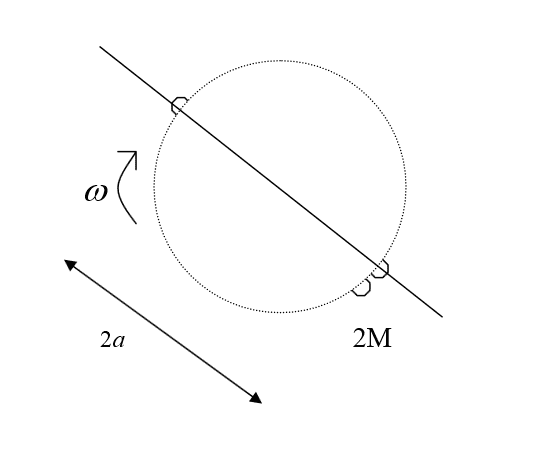
Two masses of similar mass M are connected by a rod of length 2a. the rod is rotating on a horizontal plane in an angular velocity of ω, when its center of mass (point A) is at rest. The table is horizontal and friction is neglected. (the rod is not wired to the table).
At some given time t, we locate a mass of 2M so that it sticks to one of the masses.
Question:What is the angular velocity that the rod will rotate in around its new center of mass after the collision?
What I did was this:
1. I calculated the location of the new center of mass (the after frame) and it turns out to be a/2 towards the 3M.
2. I looked at the frame just a moment before collision so that the mass 2M is really close to the mass M (one of them) but yet to collide with one. I calculated the angular momentum before collision by I*ω around the new center of mass that I stated above:
[m*(3a/2)^2 + m*(a/2)^2]*ω = 2.5m*(a^2)*ω
3. Now, I looked at the frame just a moment after the collision so the masses pretty much made no movement and again I calculated the angular velocity after collision by I*ω around the new center of mass:
[m*(3a/2)^2 + m*(a/2)^2 + 2m*(a/2)^2]*ω' = 3m*(a^2)*ω'
4. Of course there is conservation of angular momentum, therefore I equalized the two expressions to get that the new angular velocity is ω' = (5/6)*ω and not (2/3)*ω as the correct answer is.
Here's the thing that's bothering me other than that answer is wrong. I tried applying RxMV on the before system with the location of the new center of mass and it turns out to be right!
I really don't understand where have I mistaken in the solution I've given and why in A LOT of cases when I do I*ω and RxMV in this type of questions (conservation of angular momentum) I get different results. I thought they're equal...
Anyway, I'd really appreciate it if you guys told me at which point of the solution I did an incorrect step and also answer my question in the last paragraph.
THANK YOU!
I'm pretty much translating this question word by word, so if you have problem understanding something off of it, please, let me know and I'll try explaining it better.
Homework Statement
Two masses of similar mass M are connected by a rod of length 2a. the rod is rotating on a horizontal plane in an angular velocity of ω, when its center of mass (point A) is at rest. The table is horizontal and friction is neglected. (the rod is not wired to the table).
At some given time t, we locate a mass of 2M so that it sticks to one of the masses.
Question:What is the angular velocity that the rod will rotate in around its new center of mass after the collision?
Homework Equations
The Attempt at a Solution
What I did was this:
1. I calculated the location of the new center of mass (the after frame) and it turns out to be a/2 towards the 3M.
2. I looked at the frame just a moment before collision so that the mass 2M is really close to the mass M (one of them) but yet to collide with one. I calculated the angular momentum before collision by I*ω around the new center of mass that I stated above:
[m*(3a/2)^2 + m*(a/2)^2]*ω = 2.5m*(a^2)*ω
3. Now, I looked at the frame just a moment after the collision so the masses pretty much made no movement and again I calculated the angular velocity after collision by I*ω around the new center of mass:
[m*(3a/2)^2 + m*(a/2)^2 + 2m*(a/2)^2]*ω' = 3m*(a^2)*ω'
4. Of course there is conservation of angular momentum, therefore I equalized the two expressions to get that the new angular velocity is ω' = (5/6)*ω and not (2/3)*ω as the correct answer is.
Here's the thing that's bothering me other than that answer is wrong. I tried applying RxMV on the before system with the location of the new center of mass and it turns out to be right!
I really don't understand where have I mistaken in the solution I've given and why in A LOT of cases when I do I*ω and RxMV in this type of questions (conservation of angular momentum) I get different results. I thought they're equal...
Anyway, I'd really appreciate it if you guys told me at which point of the solution I did an incorrect step and also answer my question in the last paragraph.
THANK YOU!