What Is the Correct Resistance for Optimal LED Operation?

  • Thread starter Thread starter TyErd
  • Start date Start date
  • Tags Tags
    Resistance
AI Thread Summary
To achieve optimal LED operation, the correct resistance for Rl must account for the total current drawn by all LEDs. Each LED requires 20mA, and with three LEDs in parallel, the total current is 60mA. The voltage across Rl is 7V, calculated from the supply voltage minus the LED forward voltage. Using Ohm's Law, the resistance Rl should be 7V divided by 0.06A, resulting in a resistance of approximately 116.67 ohms. Proper understanding of current distribution in parallel circuits is crucial for accurate calculations.
TyErd
Messages
297
Reaction score
0

Homework Statement


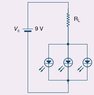
All LEDs in the following circuit are identical. Each LED has a switch on voltage of 2V and draws a current of 20mA for optimal light production.

Determine the resistance of Rl that gives optimum operation for all LEDs.


Homework Equations


Ohms Law V=IR


The Attempt at a Solution


becuase the LEDs are connected in parallel I calculated the voltage for Rl to be 9-2 =7V then divided that by 20mA which gave me 350ohms, which is incorrect.
 

Attachments

  • circuit.JPG
    circuit.JPG
    5.4 KB · Views: 367
Physics news on Phys.org


Each LED draws 20 mA current. There are three LEDs. So the total current drawn from the battery is...?
 


OMG I am an idiot, I didn't read the question properly, I thought the 20mA was divided amongst the 3 LEDs. Haha, anyway Thankyou!
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »

Thread 'Rolling without slipping on a curved surface'

Kindly see the attached pdf. My attempt to solve it, is in it. I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction. I'm not able to figure out, why my solution is wrong, if it is wrong .
View full post »

Similar threads

How to solve for EMF and internal resistance in a circuit?
Replies
8
Views
3K
Voltage, Current, and Resistance Calculations
Replies
13
Views
2K
Can a reed switch use a wheatstone bridge/potential divider?
Replies
1
Views
2K
EMF and internal resistance laboratory work
Replies
4
Views
2K
Total Resistance of Parallel Circuit Calculation
Replies
3
Views
1K
Internal Resistance of a Car Battery
Replies
8
Views
13K
Is voltage the same in parallel circuits with different resistance values?
Replies
2
Views
6K
Finding the internal resistance of battery
Replies
10
Views
3K
Physics - transformer / resistance question
Replies
4
Views
5K
What number on a digital clock draws the least current from a battery?
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top