What is the mistake in my calculation for the weight of a tapered column?

[bugatti79]

Homework Statement

Folks,

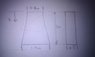
Ask to calculate the weight $W(x)$ of this tapered column at a distance x from the top as shown in the sketch.

Homework Equations

Given:
A trapezoid of bottom base 1.5m, top is 0.5m, length is 0.5m and height 2m.

Specific weight is 25kN/m^3

Area of trapezoid $A=\displaystyle \frac{h(b_1+b_2)}{2}$

The Attempt at a Solution

I have just repeated what is in the sketch for clarity.
Weight $W(x)=V* \gamma$ where $\gamma$ is the specific weight.

Area $A= \frac{x}{2}(b_1+b_2)$
$V= A*L$

Thus $W(x)=\frac{x}{2}(b_1+b_2)*L*25$

The book answer is $\displaystyle W(x)= 0.5\frac{0.5+(0.5+0.5x)}{2}x*25$

I don't understand how there x is repeated twice in the above expression.

What have I done wrong?

Regards

 

[voko]

It is unclear what is given and what you are supposed to find. Please formulate the problem properly.

 

[bugatti79]

It is unclear what is given and what you are supposed to find. Please formulate the problem properly.

I have reformulated the question as requested. Thanks

 

[voko]

What is the cross-section of the column? Circle? Square? Something else?

 

[bugatti79]

What is the cross-section of the column? Circle? Square? Something else?

I have attached the geometry of the problem. It has a front view and the rectangular side view.

Thanks

 

[voko]

OK, now it is all clear.

Let's start with the trapezoid "face" from 0 to x. What is its area? More specifically, what are its bases?

 

[bugatti79]

OK, now it is all clear.

Let's start with the trapezoid "face" from 0 to x. What is its area? More specifically, what are its bases?

Area of a quadrilateral with 1 pair of parallel sides is $\displaystyle A(x)=x \frac{(b_1+b_2)}{2}$

where $b_1$ is the bottom base and $b_2$ is the top base say..

 

[voko]

What is the bottom base for some arbitrary x?

 

[bugatti79]

What is the bottom base for some arbitrary x?

Not sure I follow.

The bottom base $b_1$ is 1.5m...?

 

[voko]

It is 1.5 only for x = 2.0. For x < 2.0, it is less than that. What is it exactly?

 

[bugatti79]

It is 1.5 only for x = 2.0. For x < 2.0, it is less than that. What is it exactly?

$A(x)=f(b_2, 0.5<b_1(x) \le 1.5)$

Not sure what $b_2$ would be exactly for some value of x! $b_2=0.5+x$..?

 

[voko]

As can be seen from the drawing, b(x) is a linear function of x. b(0) = 0.5, b(2) = 1.5. That is enough to determine it.

 

[bugatti79]

As can be seen from the drawing, b(x) is a linear function of x. b(0) = 0.5, b(2) = 1.5. That is enough to determine it.

Sorry, still don't see how the area can be calculated for some x because we don't know what the length of $b_2$ is apart from it being greater than 0.5 and less than 2...

 

[voko]

Do you see that b(x) - b(0) is proportional to x?

 

[bugatti79]

Do you see that b(x) - b(0) is proportional to x?

No, doesn't make me see the answer! I was thinking of it another way. Just take a copy of that sketch and rotate it 180degrees and put it beside it gives a parallegrom of area $h(b_1+b_2)$. We only need half of that so then actual area is $h \frac{(b_1+b_2)}{2}$

Finally, repace the h with x to give $A(x)= \frac{x}{2} (b_1+b_2)$

Im baffled by such a simple problem!

 

[voko]

Try something else. Rotate the column 90 degree counterclockwise, so that the bottom is on the right, and align it so that the middle of the column is on the X axis, and the top is at x = 0. What used to be the rightmost edge of the column is now a line above the X axis. It is a straight line. What is its equation?

 

[bugatti79]

Try something else. Rotate the column 90 degree counterclockwise, so that the bottom is on the right, and align it so that the middle of the column is on the X axis, and the top is at x = 0. What used to be the rightmost edge of the column is now a line above the X axis. It is a straight line. What is its equation?

That helps. The length of the bottom base $b_1$ is given by

$b_1(x)=2(\frac{1}{4} x+0.25)$

Thus the area of the trapezoid is $\displaystyle A(x)=\frac{x}{2} (b_1+b_2)=\frac{x}{2} (2(\frac{1}{4} x+0.25)+b_2)$...?

 

[voko]

That helps. The length of the bottom base $b_1$ is given by

$b_1(x)=2(\frac{1}{4} x+0.25)$

Thus the area of the trapezoid is $\displaystyle A(x)=\frac{x}{2} (b_1+b_2)=\frac{x}{2} (2(\frac{1}{4} x+0.25)+b_2)$...?

Correct.

 

[bugatti79]

That helps. The length of the bottom base $b_1$ is given by

$b_1(x)=2(\frac{1}{4} x+0.25)$

Thus the area of the trapezoid is $\displaystyle A(x)=\frac{x}{2} (b_1+b_2)=\frac{x}{2} (2(\frac{1}{4} x+0.25)+b_2)$...?

Ok, so the volume becomes $\displaystyle A(x)*L=\frac{x}{2} (2(\frac{1}{4} x+0.25)+b_2)*L$

The weight $W(x)$ is the volume times the specific weight ie $\displaystyle V (m^3) *\gamma (kN/m^3)= \frac{x}{2} (2(\frac{1}{4} x+0.25)+b_2)*0.5*25kN/m^3$

If we let x=1m we get $W(x)=0.375kN$ whereas the book has $W(x)= 6.25(1+.05x)x=9.375kN$..?

 

[voko]

You made a mistake in arithmetic somewhere. Your formula is correct.