sid_galt
- 502
- 1
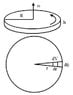
A right cylinder of radius R and height h is rotating about the yaw axis at angular velocity \theta. What is the net compression in Pascals?
I took the elemental volume as 2\pi rhdr where 2\pi rh is the lateral surface area at r. Then the radial force at a distance r from the origin is
2p\pi rh*r\theta^2dr=2p\pi r^2h\theta^2dr
where p is the density of the material of the cylinder.
Integrating it over 0 to R,
<br /> \int_0^R 2p\pi r^2h\theta^2dr=\displaystyle\frac{2p\pi h\theta^2 R^3}{3}=radial force.
Since pressure is F/A and A here is 2\pi Rh, compression is
\displaystyle\frac{2p\pi h\theta^2 R^3}{6\pi Rh}=\displaystyle\frac{p\theta^2 R^2}{3}
But \theta = \displaystyle\frac{V}{R} where V is the velocity of the boundary of the cylinder.
Thus
\displaystyle\frac{p\theta^2 R^2}{3}= \displaystyle\frac{p V^2 R ^2}{3R^2}=\displaystyle\frac{p V^2}{3}
This means compression is only dependent on the velocity of the boundary of the cylinder. I find this extremely odd and I think I have gone wrong somewhere. Where have I gone wrong?
I took the elemental volume as 2\pi rhdr where 2\pi rh is the lateral surface area at r. Then the radial force at a distance r from the origin is
2p\pi rh*r\theta^2dr=2p\pi r^2h\theta^2dr
where p is the density of the material of the cylinder.
Integrating it over 0 to R,
<br /> \int_0^R 2p\pi r^2h\theta^2dr=\displaystyle\frac{2p\pi h\theta^2 R^3}{3}=radial force.
Since pressure is F/A and A here is 2\pi Rh, compression is
\displaystyle\frac{2p\pi h\theta^2 R^3}{6\pi Rh}=\displaystyle\frac{p\theta^2 R^2}{3}
But \theta = \displaystyle\frac{V}{R} where V is the velocity of the boundary of the cylinder.
Thus
\displaystyle\frac{p\theta^2 R^2}{3}= \displaystyle\frac{p V^2 R ^2}{3R^2}=\displaystyle\frac{p V^2}{3}
This means compression is only dependent on the velocity of the boundary of the cylinder. I find this extremely odd and I think I have gone wrong somewhere. Where have I gone wrong?