What is the net torque on a wheel with given dimensions and direction?

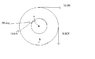
AI Thread Summary
The discussion focuses on calculating the net torque on a wheel with specified dimensions and direction, using the formula torque = force x distance. Participants calculate individual torques, noting that the 30-degree angle in the problem may be misleading. The net torque is ultimately determined to be -2.96, indicating a clockwise rotation. Clarification is provided that the 12 N force acts tangentially to the circle of radius a. The conversation highlights the importance of understanding the role of angles in torque calculations.
aaronb
Messages
22
Reaction score
0

Homework Statement


find the net torque on the wheel about the axle through O, taking a = 7.00cm and b = 20.00cm. Assume the positive direction is counterclockwise


Homework Equations


torque = force x distance
torque = force x (radius x sin(phi))


The Attempt at a Solution


10.0 x .2m = -2 (because it's moving clockwise)
9.00 x .2m = -1.8
.07 x 12 x sin(30) = .42

net torque = -3.38 (this is off by 10%-100%)
 

Attachments

  • physicshw10and11prob7.jpg
    physicshw10and11prob7.jpg
    12 KB · Views: 454
Physics news on Phys.org
I don't understand what the 30 degree angle represents.
 
Me niether, do you think it was put there to confuse?
 
aaronb said:
Me niether, do you think it was put there to confuse?
Beats me. It looks like the 12 N force is tangential to the circle of radius a. Is that the case?
 
It is there to confuse. The net torque turned out to be -2.96 so the 12N force is tangential. Thanks for bringing that up to attention
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Force on a rotating wheel/disc
Replies
25
Views
2K
Torque on a Circular Current Loop under a Misaligned Magnetic Field
Replies
1
Views
995
Calculating Net Torque on Wheel Axle
Replies
7
Views
4K
Finding the net torque about the axle?
Replies
3
Views
5K
Calculating Net Torque for an Inclined Wheel: A Problem in Applied Physics
Replies
4
Views
2K
Force exerted on counter-rotating wheels by a tennis ball
Replies
44
Views
7K
Understanding cross product and direction of torque
Replies
4
Views
2K
What is the total torque of that system?
Replies
28
Views
3K
Find the tension in the cable and reactive forces at ground
Replies
4
Views
5K
How Do You Calculate Torque on a Wrench?
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top