polymerase
- 28
- 0
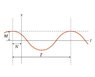
The graph shows the position x of an oscillating object as a function of time t. The equation of the graph is x(t)=Acos(wt + \phi)
where A is the amplitude, w is the angular frequency, and \phi is a phase constant. The quantities M,N, and T are measurements to be used in your answers.
See attached image.
What is \phi in the equation?
where A is the amplitude, w is the angular frequency, and \phi is a phase constant. The quantities M,N, and T are measurements to be used in your answers.
See attached image.
What is \phi in the equation?