Ravi Singh choudhary
- 123
- 7
< Mentor Note -- thread moved to HH from the technical physics forums, so no HH Template is shown >[/color]
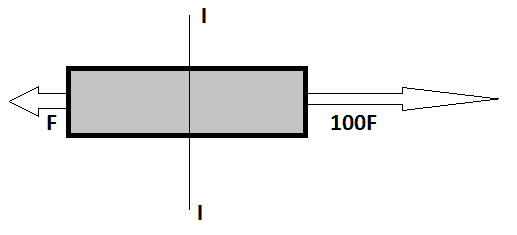
Problem Statement:
Case 1: Mass is m; Cross sectional area is uniform A. What will be the stress in the middle section.
Case 2: Bar is massless; What will be the stress in the middle section.
Case 3: Bar is still assumed massless but 100F is increased to 500F; What will be the stress in the middle section.
Relevant equation: F/A; point is to find internal force in each situation.
My attempt to the solution: I found the acceleration simply by dividing "m" to the net force "99F". My poor understanding about stress was; it only acts when body in is zero unbalanced force. Simply we have to find the internal force at point which stress need to be calculated. But I realized even after there is unbalanced force situation we have internal force at particular section.
So I solved for case I: a=(99F/m)
After solving equation F1-F=(m/2)*a; I found the value of F1 i.e. (101/2)F
stress will be F1/A.
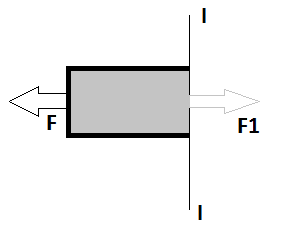
But solution given was 99F/A i.e. stress due to original force configuration at middle section.
For Case 2 and Case 3; I am clueless.
Problem Statement:
Case 1: Mass is m; Cross sectional area is uniform A. What will be the stress in the middle section.
Case 2: Bar is massless; What will be the stress in the middle section.
Case 3: Bar is still assumed massless but 100F is increased to 500F; What will be the stress in the middle section.
Relevant equation: F/A; point is to find internal force in each situation.
My attempt to the solution: I found the acceleration simply by dividing "m" to the net force "99F". My poor understanding about stress was; it only acts when body in is zero unbalanced force. Simply we have to find the internal force at point which stress need to be calculated. But I realized even after there is unbalanced force situation we have internal force at particular section.
So I solved for case I: a=(99F/m)
After solving equation F1-F=(m/2)*a; I found the value of F1 i.e. (101/2)F
stress will be F1/A.
But solution given was 99F/A i.e. stress due to original force configuration at middle section.
For Case 2 and Case 3; I am clueless.
Last edited by a moderator: