Jojo-11
- 5
- 0
- Homework Statement
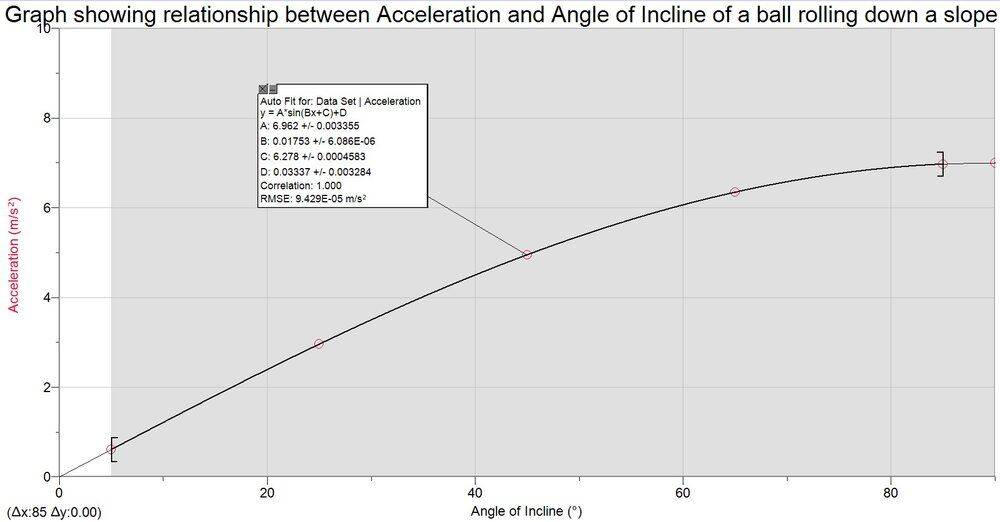
- why does acceleration of a solid sphere increase by less as the angle of incline increases?
- Relevant Equations
- a = 5mgsin𝛳/7
This is true considering the rotational inertia of a solid sphere is (2/5)mr^2
My only guess is that this is due to air resistance. Below an example of the predicted graph:
 . The ##5/7## is correct for the flat ramp. Just ignore me
. The ##5/7## is correct for the flat ramp. Just ignore me