tizzful
- 14
- 0
Two Hanging Masses (TENSION) :)
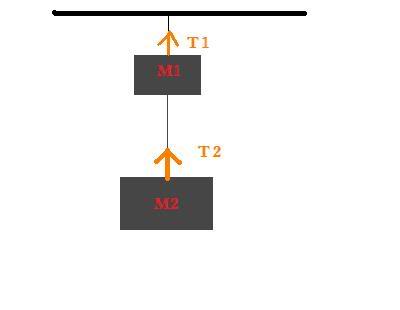
Two blocks with masses M1 and M2 hag one under the other. For this problem take the positive direction to be upward and use g for the magnitude of the acceleration due to gravity. The blocks are now accelerating upwads (due to the tension in the strings) with acceleration of magnitude a. find the tension in the lower and upper rope.
F=ma
W=mg
I found the tension in the lower and upper rope when it was stationary and therefore in equilibrium.
T2=M2g
T1=M1g
Then to find the tension when accelerating I just used
T2=Ma+Mg
T1=Ma+M1g+M2g
For some reason it says that the tension in rope 2 does not depend on the variable M1... So I'm just really lost now on which direction to take..
Thanks in advance
Homework Statement
Two blocks with masses M1 and M2 hag one under the other. For this problem take the positive direction to be upward and use g for the magnitude of the acceleration due to gravity. The blocks are now accelerating upwads (due to the tension in the strings) with acceleration of magnitude a. find the tension in the lower and upper rope.
Homework Equations
F=ma
W=mg
The Attempt at a Solution
I found the tension in the lower and upper rope when it was stationary and therefore in equilibrium.
T2=M2g
T1=M1g
Then to find the tension when accelerating I just used
T2=Ma+Mg
T1=Ma+M1g+M2g
For some reason it says that the tension in rope 2 does not depend on the variable M1... So I'm just really lost now on which direction to take..
Thanks in advance