SamRoss
Gold Member
- 256
- 36
- TL;DR Summary
- I read through "A Geometrical View of Time Dilation and the Twin Paradox" from the FAQ but I still have questions.
I feel a little guilty writing this post because I'm sure there are people here who are tired of answering questions about the twin paradox, hence the FAQ post on the subject, but there's something which is still nagging me. First I have a question about the FAQ post itself. Toward the bottom of the page, the equation
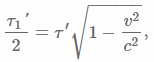 is written. There was a similar equation,
is written. There was a similar equation,
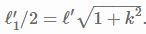 , in the prelude at the top. I'm confused by the left side of these equations. My understanding of what was meant by ##\tau^{'}_1## and ##l^{'}_1## was that they were the lengths of the red line segments in the diagrams, so the effect of putting them over 2 would be to cut them in half. But this is precisely what was said to be an error. That is, ##\tau^{'}_1/2## and ##l^{'}_1/2## are not half the length of the line segments. Could someone straighten this out for me?
, in the prelude at the top. I'm confused by the left side of these equations. My understanding of what was meant by ##\tau^{'}_1## and ##l^{'}_1## was that they were the lengths of the red line segments in the diagrams, so the effect of putting them over 2 would be to cut them in half. But this is precisely what was said to be an error. That is, ##\tau^{'}_1/2## and ##l^{'}_1/2## are not half the length of the line segments. Could someone straighten this out for me?
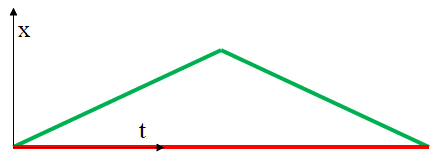
Okay, now for what's really nagging me. I feel like this really gets to the heart of why schmucks like me can't wrap our heads around the paradox (or maybe it's just me). Despite the confusion I described above, I think the FAQ post did a pretty good job of shedding light on the issue. We start with a set of perpendicular axes and calculate the proper times for the red (stays on Earth) observer and green (flies off and comes back) observer. We see that the proper time for the red guy is greater than the proper time for the green guy. Then we switch to oblique axes, we work through it again, and voila! The proper time of the red guy is still bigger. I know I should be satisfied by this but there's something that still troubles me and, like I said, I think it gets to the heart of what's so unsettling about the paradox. Why is the green guy always the bent one? Here's what the basic diagram looked like in the FAQ...
 Now I know I must be wrong somewhere, but it really really feels like we ought to be able to draw a diagram like this...
Now I know I must be wrong somewhere, but it really really feels like we ought to be able to draw a diagram like this...
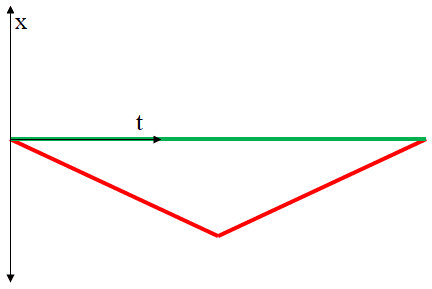
In this case, the green guy looks like he's staying put while the red guy moves first in the negative direction and then back. It seems like we should be able to go through all the same steps that were explained in the FAQ and discover that this time the green guy's proper time is the greater one whether we use perpendicular or oblique axes. Something tells me I can't be the only one who is thinking along these lines so if anyone can explain where the error in my reasoning is, you'd not only be helping me out but maybe others as well. Perhaps an explanation could be added to the FAQ.
Okay, now for what's really nagging me. I feel like this really gets to the heart of why schmucks like me can't wrap our heads around the paradox (or maybe it's just me). Despite the confusion I described above, I think the FAQ post did a pretty good job of shedding light on the issue. We start with a set of perpendicular axes and calculate the proper times for the red (stays on Earth) observer and green (flies off and comes back) observer. We see that the proper time for the red guy is greater than the proper time for the green guy. Then we switch to oblique axes, we work through it again, and voila! The proper time of the red guy is still bigger. I know I should be satisfied by this but there's something that still troubles me and, like I said, I think it gets to the heart of what's so unsettling about the paradox. Why is the green guy always the bent one? Here's what the basic diagram looked like in the FAQ...
In this case, the green guy looks like he's staying put while the red guy moves first in the negative direction and then back. It seems like we should be able to go through all the same steps that were explained in the FAQ and discover that this time the green guy's proper time is the greater one whether we use perpendicular or oblique axes. Something tells me I can't be the only one who is thinking along these lines so if anyone can explain where the error in my reasoning is, you'd not only be helping me out but maybe others as well. Perhaps an explanation could be added to the FAQ.