- #1
themli
- 21
- 3
Member warned that the homework template is required
If a brick is pulled across the floor by a rope thruogh a pulley, 1 meter above the ground - and work = W, where [itex]W = 10N [/itex], (in Newton).Show that the horizontal component of W, which is pulling the brick has the size
[tex] \frac{10x}{\sqrt{1+x^2}} (*) [/tex]
Use this to calculate the amount of work needed to move the brick from x = 10 to x = 2.
This is what I have so far:
In terms of the expression (*), I'm thinking the 10x has to do with W being equal to 10N, and the W-side (call it Z) being the hypotenuse: [itex] \sqrt{1+x^2} [/itex]
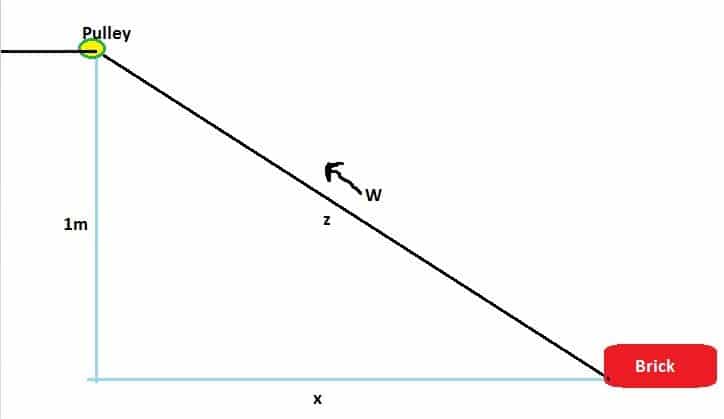
Let the angle by the brick be θ:
[tex] \cos θ=\frac{x}{\sqrt{1+x^2}} [/tex]
So is the formula found by taking cosθ×10?
In terms of calculating work, I'm not sure. I first thought taking the definite integral of (*) from 2 to 10?
[tex] \frac{10x}{\sqrt{1+x^2}} (*) [/tex]
Use this to calculate the amount of work needed to move the brick from x = 10 to x = 2.
This is what I have so far:
In terms of the expression (*), I'm thinking the 10x has to do with W being equal to 10N, and the W-side (call it Z) being the hypotenuse: [itex] \sqrt{1+x^2} [/itex]
Let the angle by the brick be θ:
[tex] \cos θ=\frac{x}{\sqrt{1+x^2}} [/tex]
So is the formula found by taking cosθ×10?
In terms of calculating work, I'm not sure. I first thought taking the definite integral of (*) from 2 to 10?
Last edited by a moderator:
 : should of course be ##\ \cot\theta = x \ ##
: should of course be ##\ \cot\theta = x \ ##