X and Y components of a vector using a graph of speed/time

[AidenPhysica]

Homework Statement

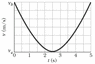
A golf ball is struck at ground level. The speed of the golf ball as a function of the time is shown in the figure, where t = 0 at the instant the ball is struck. The scaling on the vertical axis is set by va= 16 m/s and vb= 29.3 m/s. (a) How far does the golf ball travel horizontally before returning to ground level? (b) What is the maximum height above ground level attained by the ball?
[PLAIN]https://edugen.wileyplus.com/edugen/courses/crs7165/art/qb/qu/c04/fig04_40.gif[/B]

Homework Equations

x component=|magnitude of vector|cos(theta)
y component=|magnitude of vector|sin)theta)
s=.5(v0+v)t

The Attempt at a Solution

16 m/s is the minimum value on this graph and 29.3 is the maximum value on this graph. 29.3 appears first and then 16 is in the middle in a concave-up parabola. So this is what I did and I wonder if this is right:
So the initial velocity, a mixture of both x and y components is=29.3. To find the theta, we can take 29.3cos(theta)=16. Why do we use 16? Because the minimum speed corresponds to a vertical velocity of 0, meaning 16 is the constant horizontal velocity. So then, theta is =56.91 degrees. We then have to solve for initial y component of velocity, so we have 29.3sin(56.91)=24.55. We then say, since the graph has 5 seconds at the end point: s=.5(16+16)*5=80m. Is that right? for a. And then is b just s=.5(24.546+0)*2.5=30.6825? Thanks for the help, I just am unsure. Thanks and have great day :)

 

[AidenPhysica]

The image of the graph is attached below:

 

[TomHart]

Looks right to me.