- #1
cupid.callin
- 1,132
- 1
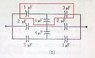
This was a ques in my book ... (Pic)
After thinking a while, i realized that it can be solved using Y-Delta (by converting Y to delta form) conversion. But i couldn't get the answer ... i don't know why ...
I used this http://en.wikipedia.org/wiki/Y-%CE%94_transform"
It is given for resistors ... i guess its same for resistors and capacitors ... Right?
Please tell me if the eqn used is wrong or something else!
After thinking a while, i realized that it can be solved using Y-Delta (by converting Y to delta form) conversion. But i couldn't get the answer ... i don't know why ...
I used this http://en.wikipedia.org/wiki/Y-%CE%94_transform"
It is given for resistors ... i guess its same for resistors and capacitors ... Right?
Please tell me if the eqn used is wrong or something else!
Attachments
Last edited by a moderator: