jamiewilliams
- 11
- 0
Homework Statement
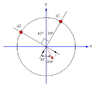
The drawing shows two positive charges q1 and q2 fixed to a circle. At the center of the circle they produce a net electric field that makes an angle 28.6° with the vertical axis, measured counterclockwise. Determine the ratio q2/q1.
[the drawing shows a circle with two charges: q1 measures 30° from the vert and q2 (on the other side of the vertical axis) measures 60° from the vert]
Homework Equations
Coulomb's Law
?
The Attempt at a Solution
First I sketched the situation and drew 2 vectors coming from the origin for the energy fields E1 and E2 (from q1 and q2, respectively). I drew the x and y components of each vector using trig functions. I think I am on the right track but I am stuck! No matter how I move around the equations and/or algebra I can't seem to get the right answer.
[correct answer is 1.64]