Distribution of charge in two charged capacitors joined in a circuit

[thisischris]

Hello!

I'm having a bit of a struggle understanding the logic behind these two questions.

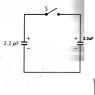
A 2.2 uF capacitor is charged to a potential of 15V, and a 3.3uF capacitor is charged to a potential of 30V.
The capacitors are then joined together as in the circuit diagram. When the switch s is closed, the charge re-distributes between the capacitors. Explain why the final voltage across each capacitor is the same.

Answer: Capacitors are in parallel.

I sort of agree that the voltage would be the same otherwise charge would 'flow' from one point to another. I don't understand how them being in parallel explains this however.

Suggest why the calculated value of energy stored by the capacitors (1.6 x10^-3J) is less than the total energy that would be stored by the capacitors individually.

Answer: Work is done redistributing charge.

Is this due to resistance/internal resistance(?). However we haven't accounted for it (I think?) so I don't see why it should be lower, unless the question refers to a actual experiment that may take place?


Thank you

 

[mfb]

After connecting both capacitors, you have a voltage between the lower and the upper wire (where I do not care about its value here). Both capacitors are connected to them (in parallel), therefore they both have this voltage.

Is this due to resistance/internal resistance(?)

It is. With ideal components, you get unphysical results. However, in reality you usually have some resistance somewhere (wires, switch, capacitors). If you carefully avoid all of them, the small inductance of the system can give you a resonator and it takes a while to reach equilibrium. Anyway, you can calculate the equilibrium voltage and the corresponding energy, and you know that some energy has to leave the system in order to reach this state.

 

[truesearch]

When capacitors are charged or discharged energy is lost in the process. Energy is lost in the connecting wires and any resistance in the circuit. Energy lost in the wires can be heating due to the resistance of the wires and electro magnetic radiation from the wires due to the changing current during charging/discharging.

 

[Ratch]

Chris,

I sort of agree that the voltage would be the same otherwise charge would 'flow' from one point to another. I don't understand how them being in parallel explains this however.

When they are in parallel, both ends of the two capacitors are connected to the same two points. Therefore, they have to be at the same voltage. That is not true for series connected caps.

Is this due to resistance/internal resistance(?). However we haven't accounted for it (I think?) so I don't see why it should be lower, unless the question refers to a actual experiment that may take place?

If you assume no circuit resistance, then no energy will be lost. But then you also have to assume the the equalization current will be infinite. That can never happen in a practical circuit, so the final energy will always be less the initial value.

Ratch

 

[thisischris]

Thank you for everyone's help. Much appreciated. :)