2 springs @ 30 degrees supporting a mass

[alaix]

Homework Statement

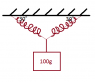
A mass of 100g is supported by two identical springs of negligible mass having spring constants k= 50 dynes/cm. In the equilibrium position, the springs make an angle of 30 degree with the horizontal and are 100 cm in length. If the mass, m, is pulled down a distance of 2cm and released, find the period of the resulting oscillation.

Homework Equations

\sum F = ma

F_{s} = -kx

x = A cos(\omega t) + B sin(\omega t)

\omega = \sqrt{k/m}

P = 2\pi / \omega = 2\pi \sqrt{m/k}

The Attempt at a Solution

I tried different approaches for this one. I started by taking the last formula I gave.

The y component of the restoring force is equal to half the restoring force (30 degree angle, sin(30) = 1/2.
Since we have 2 strings, I multiplied k by 2 in this equation, which gave me:

P = 2\pi \sqrt{100/2*50*cos(30)} = 2\pi \sqrt{100/50} = 4\pi

I find this way too simple so I guess this isn't right...


Other things I tried:
I found that the diagonal "movement" in this case was 1.99 (extension = 101.01, compression = 99.02) using pythagorean theorem.

I then use the 2nd Newton law:

ma = -kx
100*a = -50x
a = -1/2x
a+1/2x = 0

x = A cos(\omega t) + B sin(\omega t)
Initial conditions: x = 1,01 a = 0 @ t = 0

Therefore

x = 1.01 cos(\sqrt(1/2) t)

P = 2\pi / \sqrt{1/2} = 8.886



Is any of this any good? I don't have the answer to this exercise so I have no clue if I'm even in the good direction...

Thanks!

Alaix

 

[Spinnor]

Does this look like the right way to solve your problem?

 

[alaix]

Does this look like the right way to solve your problem?

So if I get this right, you want me to take the "Effective spring constant" which would be 4 k sin(30)² and "inject" it into the equation

P = 2pi sqrt(m/k)

Also I'm not sure where the whole mg = 2T sin(30) is related to the rest of your maths...

I guess this make some kind of sense. Would appreciate a second opinion about this :)

Thanks

 

[alaix]

Any other suggestion?

 

[Spinnor]

If you have a mass, m, connected to a spring of spring constant k and you displace the mass and let it go that is the end of the story. See,

http://en.wikipedia.org/wiki/Harmonic_oscillator

The trick for your problem is coming up with the effective value of k which if I did not come up with the right answer at least I think I was heading in the right direction. As for the equality I wrote down,

mg = 2T sin(30)

turns out I did not use it. You right down stuff you know, maybe you use it.

Good luck!

 

[alaix]

In a simpler way, could we possibly say that 2 springs @ 30 degrees would do the same thing as one identical spring @ 90 degrees?

 

[anigeo]

effective spring constant of the spring = 50sin(30)+50sin(30)=50 dyne/cm.
force=980*100=9.8*10^4 dyne.
F=kx
→98000=50*x
→x=19.6 m.

 

[alaix]

effective spring constant of the spring = 50sin(30)+50sin(30)=50 dyne/cm.
force=980*100=9.8*10^4 dyne.
F=kx
→98000=50*x
→x=19.6 m.

How does that make any sense?

 

[alaix]

Here is what my teacher answered me:

You need to consider the extension of the spring in the 2nd Newton Law but keep everything as symbols. Be careful for the vertical projection of the tensions in both springs during the oblique extension. Redo 2nd Newton Law and be looking for a spring that is the equivalent of the 2 others (it has a different spring constant).

At the end, you have to do a dramatic approximation on this general extension to make the process simpler. The equilibrium condition is important and can always be useful


Using the spring constant Spinnor found, I find that effective K = k and therefore a period of 8.88sec which is NOT good...

More help would really be appreciated

 

[Spinnor]

If you followed my sketch, k effective was k/2, or 25 dynes/cm

Does that work? 8^)

 

[alaix]

That would actually make a period 0f 12 seconds... Since it's less than 8, I doubt that's the proper way :S