Gourab_chill
- 55
- 3
- Homework Statement
- I have posted the question as a attachment below. Please open the attachment to find the question.
- Relevant Equations
- Q=CV, Kirchoff's voltage law
In my opinion, the voltage across the C1 should be 9V as the potential on the side of the positive plate of the capacitor should be (15-6)V and on the other be 0V.
Similarly the potential across C2 should be (7-0)V.
Here I'm basically assuming that the voltage at the negative terminals of the cells to be zero, which is the point I'm mistaking probably. The answer to the question is-
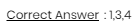
Please tell how to approach this question. Any help will be deeply appreciated.
Similarly the potential across C2 should be (7-0)V.
Here I'm basically assuming that the voltage at the negative terminals of the cells to be zero, which is the point I'm mistaking probably. The answer to the question is-
Please tell how to approach this question. Any help will be deeply appreciated.
