marstery
- 11
- 0
The problem is in bold and my logic/answers/questions are below. Please check my logic and any help with my uncertainties would be...well, helpful. thx
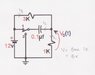
The switch has been in position 1 for a long time. Determine the voltage drop Vc(0) and V0(0-).
Since it has been a long time the capacitor acts as an open circuit so the current through the capacitor is 0ma and the current around the outer window is 12v/4k=3ma so V0(0-) is 3v. Current Ic is zero but was flowing to the right (contrary to the arrow drawn). Vc(0) is 12v since it has been a long time and the capacitor has charged fully.
The switch is thrown to position two at t=0. What is V0(0+)?
At t=0 the capacitor acts as a short and discharges in the direction that Ic is drawn. I3 is now 4ma. Since the cap is a short does all of the current flow into the cap so that V0(0+) is 0v for that moment?
Find the time constant and V0(t>5tc).
t=RC=3k*0.1 \mu[\tex]f=300\mu[\tex] s and after 5tc the capacitor is once again fully charged so all of the current is going the R1 and R2 so that V0(t&gt;5tc) is 3v again.<br /> <br /> <b>write an expression for V0(t&gt;=0)</b><br /> <br /> it will look like a logarithmic curve starting at 0 and leveling at (3 or -3v??) after 5tc, but i don&#039;t really know the eq for it.
The switch has been in position 1 for a long time. Determine the voltage drop Vc(0) and V0(0-).
Since it has been a long time the capacitor acts as an open circuit so the current through the capacitor is 0ma and the current around the outer window is 12v/4k=3ma so V0(0-) is 3v. Current Ic is zero but was flowing to the right (contrary to the arrow drawn). Vc(0) is 12v since it has been a long time and the capacitor has charged fully.
The switch is thrown to position two at t=0. What is V0(0+)?
At t=0 the capacitor acts as a short and discharges in the direction that Ic is drawn. I3 is now 4ma. Since the cap is a short does all of the current flow into the cap so that V0(0+) is 0v for that moment?
Find the time constant and V0(t>5tc).
t=RC=3k*0.1 \mu[\tex]f=300\mu[\tex] s and after 5tc the capacitor is once again fully charged so all of the current is going the R1 and R2 so that V0(t&gt;5tc) is 3v again.<br /> <br /> <b>write an expression for V0(t&gt;=0)</b><br /> <br /> it will look like a logarithmic curve starting at 0 and leveling at (3 or -3v??) after 5tc, but i don&#039;t really know the eq for it.
Last edited: