Jeremy Sawatzky
- 29
- 11
- TL;DR Summary
- I need to apply 4500lbs of force to a belt using an air cylinder and a lever Assembly. How do I calculate the required air cylinder size?
Hi, I am looking for some guidance on how to approach this calculation. I have an air cylinder operating a lever assembly that then applies pressure to a pulley of which a belt is wrapped around. I need the belt to have about 4500 lbs of tension. How do I work backwards to figure the required power of the air cylinder?
In the first image, the belt will be totally slack so effectively I am only overcoming the friction of the pivot points and the sleeve guides that support the pulley assembly. I have prior experience with this assembly and know the friction to be negligible and not important to the initial movement of this assembly. However I am sure that it plays a part later on.
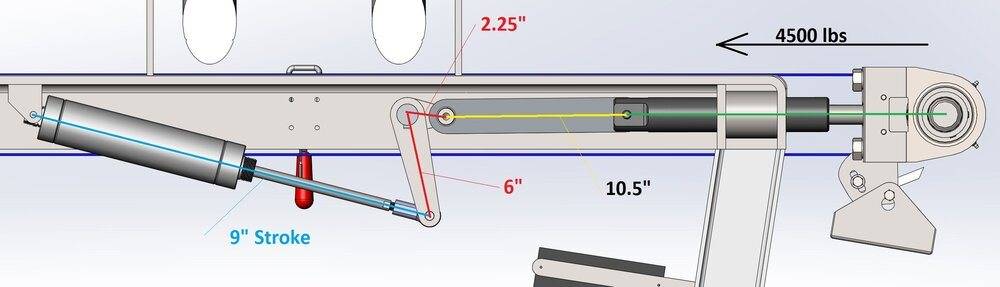
In the second image, the air cylinder is fully extended putting the full tension on the belt. The belt is returning 4500lbs of force. The belt tension increases rapidly towards the end of the air cylinder stroke as it barely stretches at all. I would hazard a guess that 99% of the work is done in the last 3" of the air cylinder stroke.
Thanks!
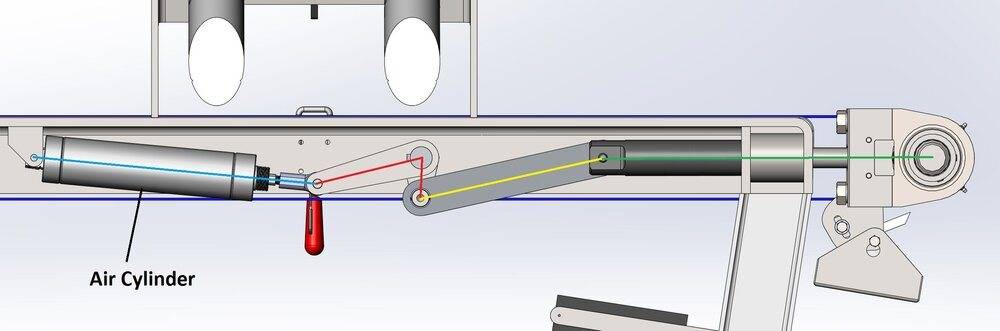
In the first image, the belt will be totally slack so effectively I am only overcoming the friction of the pivot points and the sleeve guides that support the pulley assembly. I have prior experience with this assembly and know the friction to be negligible and not important to the initial movement of this assembly. However I am sure that it plays a part later on.
In the second image, the air cylinder is fully extended putting the full tension on the belt. The belt is returning 4500lbs of force. The belt tension increases rapidly towards the end of the air cylinder stroke as it barely stretches at all. I would hazard a guess that 99% of the work is done in the last 3" of the air cylinder stroke.
Thanks!
Last edited by a moderator: