Brilli
- 48
- 0
Homework Statement
This is a practice olympiad problem
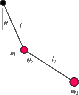
A light rod with length l is
hinged in such a way that the hinge folds
in one plane only. The hinge is spun with
angular speed ω around a vertical axis. A
small ball is fixed to the other end of the
rod. (a) Find the angular speeds for which
the vertical orientation is stable. (b) The
ball is now attached to another hinge and,
in turn, to another identical rod; the upper
hinge is spun in the same way. What is
now the condition of stability for the ver-
tical orientation?
Homework Equations
The Attempt at a Solution
balancing torques of lower ball, got
w=g (sina)/(sina+sinb) a and b are deviations from verical of upper and lower ball respectively. Then for the upper ball equating torques of thread tension of lower thread and mass and centridugal force. But i am stuck here. The solution says to derive expression for potential energy and get for what w is it minimum because forequilibrium the potential energy isminimum. How to derive this?