Xlorep
- 2
- 0
Note: This is similar to 2 previous questions I've seen here (https://www.physicsforums.com/showthread.php?t=261193"), and while this is my first post, I've lurked/found this site to really be helpful in getting me to be able to figure out how to solve problems I have with my physics homework.
Two pulley wheels, one of radius 0.3 m and the other of radius 0.82 m, are mounted rigidly on a common axle. The rotational intertia of the two pulleys, which are clamped together, is 3.3 kg·m². A mass of 44 kg mass is attached on the left and a mass of 37 kg mass on the right, as shown.
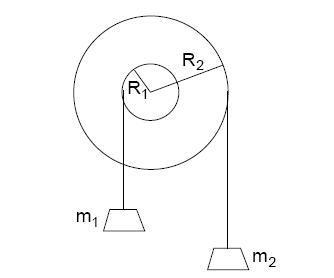
Find the angular acceleration of the system. Take the clockwise direction to be positive. The acceleration of gravity is 9.8 m/s². Answer in units of rad/s².
ΣΤ = Iα
ΣΤ = Τ1 + Τ2
So, the process I followed was this:
I found the torques for each mass & radius:
Τ1 = -(m1)g(R1)sin(90) --> (negative because going CCW)
Τ2 = (m2)g(R2)sin(90) --> (positive because going CW)
Therefore: ΣΤ = (m2)g(R2) - (m1)g(R1) = g(m2R2 - m1R1)
Which means: g(m2R2 - m1R1) = Iα
α = g(m2R2 - m1R1)/I
Checking the units, I should get rad/s²:
m/s²·(kg·m)/kg·m²
Which is: (m²·kg)/(s²·kg·m²)
Results in: rad/s²
So my units check out.
So, with the following variables (I'm hoping I got the left/right values correct):
Plugging these in, I get:
α = [9.8]([37][0.82] - [44][0.3])/[3.3]
α = (9.8)(30.34 - 13.2)/3.3
α = (9.8)(17.14)/3.3
α = (167.972)/3.3
α = (167.972)/3.3
α = 50.90060606 rad/s²
Which, apparently, is wrong. So I'm at a loss. What did I do wrong? Or rather, what would be a good hint for me to figure out where I went wrong?
(and yes, I know it seems strange for an α > g... that doesn't seem to logically follow for me)
Homework Statement
Two pulley wheels, one of radius 0.3 m and the other of radius 0.82 m, are mounted rigidly on a common axle. The rotational intertia of the two pulleys, which are clamped together, is 3.3 kg·m². A mass of 44 kg mass is attached on the left and a mass of 37 kg mass on the right, as shown.
Find the angular acceleration of the system. Take the clockwise direction to be positive. The acceleration of gravity is 9.8 m/s². Answer in units of rad/s².
Homework Equations
ΣΤ = Iα
ΣΤ = Τ1 + Τ2
The Attempt at a Solution
So, the process I followed was this:
I found the torques for each mass & radius:
Τ1 = -(m1)g(R1)sin(90) --> (negative because going CCW)
Τ2 = (m2)g(R2)sin(90) --> (positive because going CW)
Therefore: ΣΤ = (m2)g(R2) - (m1)g(R1) = g(m2R2 - m1R1)
Which means: g(m2R2 - m1R1) = Iα
α = g(m2R2 - m1R1)/I
Checking the units, I should get rad/s²:
m/s²·(kg·m)/kg·m²
Which is: (m²·kg)/(s²·kg·m²)
Results in: rad/s²
So my units check out.
So, with the following variables (I'm hoping I got the left/right values correct):
- g = 9.8 m/s²
- m1 = 44 kg
- R1 = 0.3 m
- m2 = 37 kg
- R2 = 0.82 m
- I = 3.3 kg·m²
Plugging these in, I get:
α = [9.8]([37][0.82] - [44][0.3])/[3.3]
α = (9.8)(30.34 - 13.2)/3.3
α = (9.8)(17.14)/3.3
α = (167.972)/3.3
α = (167.972)/3.3
α = 50.90060606 rad/s²
Which, apparently, is wrong. So I'm at a loss. What did I do wrong? Or rather, what would be a good hint for me to figure out where I went wrong?
(and yes, I know it seems strange for an α > g... that doesn't seem to logically follow for me)
Last edited by a moderator: