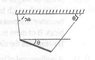
- #1
Vibhor
- 971
- 40
Homework Statement
Note : In the above setup the string lengths are unequal and the left angle is 30° and right angle is 60° .
Homework Equations
The Attempt at a Solution
[/B]
Just after the string is cut , writing force eq. for rod in vertical direction .
##Mg - Tcos60° = Ma_y ## (1)
Writing force eq in horizontal direction
##Tsin60° = Ma_x## (2)
Writing torque eq about the CM of the rod ,
##Tcos 60°\frac{L}{2} = \frac{ML^2}{12} \alpha ## (3)Writing constraint eq. for the left end point of the rod where string is attached ,the component of acceleration of left end along the string length should be zero .
##a_ycos60° - \frac{αL}{2}cos60° - a_xcos30°= 0 ## (4)Solving the above four eqs .give ##T= \frac{2}{7}Mg##
and ##\alpha = \frac{6g}{7L}##
Could someone check my work ?
 .
.