- #1
yoni162
- 16
- 0
Homework Statement
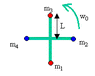
4 masses are attached to a rotating cross. At some point, mass 4 is detached from the cross. What will be the angular velocity w' in which the 3 remaining masses will rotate about their center of mass (with the cross, which has no mass)?
Homework Equations
L(0)=L(of masses relative to center of mass)+L(center of mass itself relative to 0)
The Attempt at a Solution
At first I calculated the angular momentum L1 = Iw (w is given). Next, I used the above formula, with a little addition. I calculated the angular momentum of the 3 masses relative to THEIR center of mass, calculated the angular momentum of their center of mass relative to 0 (the point where the first angular momentum was calculated, before the separation - 0), and to that I added the angular momentum of the fourth mass (which was detached) relative to 0. I then summed all three components. Meaning I got:
L2(relative to lab)=L(3 masses relative to their center of mass)+L(center of mass of 3 masses, relative to 0)+L(fourth mass, relative to 0). Then I wrote L1=L2.
I just want to know if this attempt is valid..
Attachments
Last edited: