Band Pass Filter Transfer Function Analysis

[pcrmx]

Homework Statement

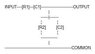
A band Pass filter is given with the following configuration, R-Resistor, C-Capacitor:

See Attatchment 1 - Circuit.jpg
https://www.physicsforums.com/attachment.php?attachmentid=16241&stc=1&d=1225999965

R1 = R2 = 10 kΩ

C1 and C2 are unknown

Cut off Frequencies are: F1 = 180 Hz, F2 = 5500 Hz

Homework Equations

The Attempt at a Solution

The transfer function derived is below:

see Attatchment 2 - tf.jpg

https://www.physicsforums.com/attachment.php?attachmentid=16242&stc=1&d=1225999965

I have been informed that it can be assumed that ([C2 x R2] / C1) can effectively = 0, due to the fact that at the centre frequency the circuit effectively becomes a voltage divider, and at this point the gain would equal 1.

However I am unsure of how to derive the values of C from there, I have attempted to do make ([C2 x R2] / C1) = 0 and then put in values for omega, twice, once for each value of omega, and then tried using simultaneous equations to solve the c values, but with their being 2 values for omega I am getting stuck at a few points.

Any help would be greatly appreciated, thanks.

 

[CEL]

At the two cutoff frequencies the real and imaginary parts of the denominator of the TF must be equal.
You have two equations, so you can calculate two unknowns. Since you have 4 unknowns, you can assign arbitrary values to your capacitors and calculate the values of the resistors.

 

[pcrmx]

At the two cutoff frequencies the real and imaginary parts of the denominator of the TF must be equal.
You have two equations, so you can calculate two unknowns. Since you have 4 unknowns, you can assign arbitrary values to your capacitors and calculate the values of the resistors.

I don't follow, I already have the value of the resistors, I understand that I have to use two equations, with each omega value, but when you get to simultaneous equations I can re-arrange to get say C1, but then to get C2 what value of omega would I substitute into get that value. Previously you have used the two values to get the C1 value?

 

[CEL]

I don't follow, I already have the value of the resistors, I understand that I have to use two equations, with each omega value, but when you get to simultaneous equations I can re-arrange to get say C1, but then to get C2 what value of omega would I substitute into get that value. Previously you have used the two values to get the C1 value?

If you already have the values of the resistors, use the two equations to get C1 and C2.
In one equation you use \omega=2 \pi 180. In the other \omega=2 \pi 5500.

 

[pcrmx]

If you already have the values of the resistors, use the two equations to get C1 and C2.
In one equation you use \omega=2 \pi 180. In the other \omega=2 \pi 5500.

Yes I get that part, but once you have a value of say C1, then in order to find C2 you must put C1 into the original equation. This original equation also has omega in it, for which I have two values. I am unsure of what value of omega to use, as I can get two values for C2 from this.

 

[CEL]

Yes I get that part, but once you have a value of say C1, then in order to find C2 you must put C1 into the original equation. This original equation also has omega in it, for which I have two values. I am unsure of what value of omega to use, as I can get two values for C2 from this.

You work with the two equations simultaneously, each one with one value of the frequency. Two equations with two unknowns.

 

[pcrmx]

You work with the two equations simultaneously, each one with one value of the frequency. Two equations with two unknowns.

Thanks for your help, appreciate it.