adam199
- 17
- 0
Picture of the problem:
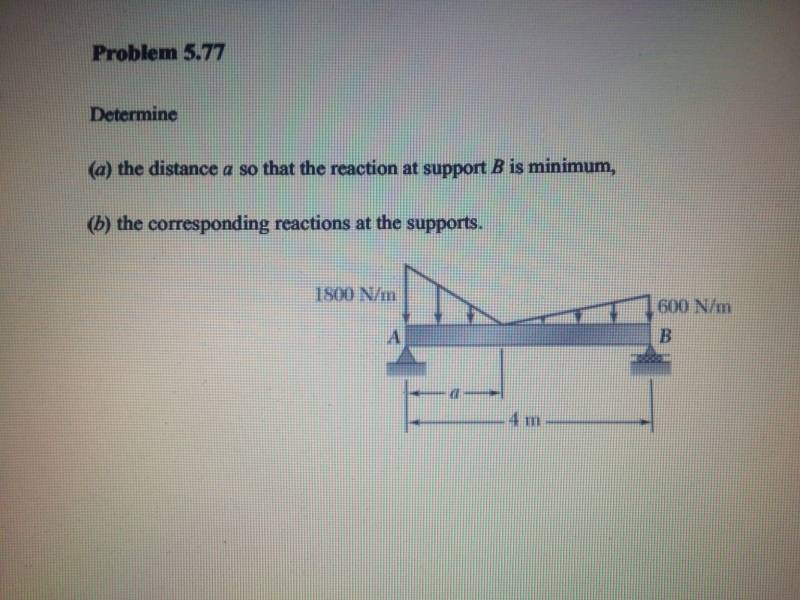
Relevant equations are the ones used to find the reactions at the supports (moment about points, forces in the x and y) and the ones used to determine the centroid.
I'm having a hard time finding a. I found the moment of area for each triangle, with the origin at A, and the sum of the areas turned out to be ƩA=1200+600a and ƩxA=200a^2-400a+3200. I know that the coordinate X of the centroid can be found by dividing ƩxA by ƩA, and doing so brought me no closer to finding a. I then tried to set up the equations for the moment about point A, Fy, and Fx and got:
Ma=500a^2-400a+3200-4By=0 (By is the reaction force at point B in the y-direction)
Fx=0, Ax=0 (since all other forces, including the roller at point B, are vertical)
Fy=Ay+By-(1200+600a)=0 (where the 1200+600a is the combined load applied to the beam, figured out from the centroid stuff earlier)
I can't figure out how to manipulate the centroid or moment/force equations to obtain a. Any help would be much appreciated.
Relevant equations are the ones used to find the reactions at the supports (moment about points, forces in the x and y) and the ones used to determine the centroid.
I'm having a hard time finding a. I found the moment of area for each triangle, with the origin at A, and the sum of the areas turned out to be ƩA=1200+600a and ƩxA=200a^2-400a+3200. I know that the coordinate X of the centroid can be found by dividing ƩxA by ƩA, and doing so brought me no closer to finding a. I then tried to set up the equations for the moment about point A, Fy, and Fx and got:
Ma=500a^2-400a+3200-4By=0 (By is the reaction force at point B in the y-direction)
Fx=0, Ax=0 (since all other forces, including the roller at point B, are vertical)
Fy=Ay+By-(1200+600a)=0 (where the 1200+600a is the combined load applied to the beam, figured out from the centroid stuff earlier)
I can't figure out how to manipulate the centroid or moment/force equations to obtain a. Any help would be much appreciated.
Last edited: