potatogirl
- 8
- 1
- Homework Statement
- Consider a fixed point charge of +1.50 μC (q1). A 2nd point charge, q3, of -0.50 μC is placed .500m to the right of q1. Finally, a third point charge q3, of -1.00 μC is placed exactly half way between q1 and q2, and moved down .300m downward. What is the magnitude and direction of the electric force exerted on q3?
- Relevant Equations
- Electric Force = Kc*q1*q2/r^2
So for this problem I think I am doing something weird with the trig and/or vector components. I calculated the problem like this:
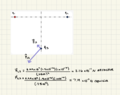
First drew a picture, q1 and q2 on the x axis. q3 located equidistant between them but negative .300m in the y direction.
First finding magnitude of Electric Force due to q1 and q3, and due to q2 and q3:
|F13|= 8.99*10^9(1.5*10^-6C)(1*10^-6C)/(.25m^2 + .3m^2) = 8.826 *10^-2 N
|F23|= 8.99*10^9(.5*10^-6C)(1*10^-6C)/(.25m^2 + .3m^2) = 2.9475 *10^-2 N
Then found angle theta using arctan(.3/.25) = 50.19 degrees (this might be part of the problem)
Then broke down F13 and F23 into x and y components:
F13x= 8.826 *10^-2cos(50.19) = 5.68 * 10^-2 î
F13y= 8.826 *10^-2sin50.19) = 6.77*10^-2 ĵ
F23x= 2.9475*10^-2cos(50.19) = 1.89*10^-2 î
F23y= 2.9475*10^-2sin(50.19) = 2.26*10^-2 ĵ
Finally, adding up ĵ and î components respectively, yields: 7.57*10^-2 N î + 9.03*10^-2 N ĵ
With respect to what angle, have no idea, I don't remember how to find that. I think that my angle of 50 degrees needs to be adjusted by subtracting it from 180 degrees or something but that doesn't seem to make sense either.
For reference, the solution should be:
|F| = 0.088𝑁 ∠ 149° w/r +x
Which obviously is not in component form, but I still don't know how they got that magnitude or direction. I did notice that is is close to my answer in the y direction, which makes me feel like maybe x-components cancel here?
Anyways, any help would be appreciated! Thank you.
First drew a picture, q1 and q2 on the x axis. q3 located equidistant between them but negative .300m in the y direction.
First finding magnitude of Electric Force due to q1 and q3, and due to q2 and q3:
|F13|= 8.99*10^9(1.5*10^-6C)(1*10^-6C)/(.25m^2 + .3m^2) = 8.826 *10^-2 N
|F23|= 8.99*10^9(.5*10^-6C)(1*10^-6C)/(.25m^2 + .3m^2) = 2.9475 *10^-2 N
Then found angle theta using arctan(.3/.25) = 50.19 degrees (this might be part of the problem)
Then broke down F13 and F23 into x and y components:
F13x= 8.826 *10^-2cos(50.19) = 5.68 * 10^-2 î
F13y= 8.826 *10^-2sin50.19) = 6.77*10^-2 ĵ
F23x= 2.9475*10^-2cos(50.19) = 1.89*10^-2 î
F23y= 2.9475*10^-2sin(50.19) = 2.26*10^-2 ĵ
Finally, adding up ĵ and î components respectively, yields: 7.57*10^-2 N î + 9.03*10^-2 N ĵ
With respect to what angle, have no idea, I don't remember how to find that. I think that my angle of 50 degrees needs to be adjusted by subtracting it from 180 degrees or something but that doesn't seem to make sense either.
For reference, the solution should be:
|F| = 0.088𝑁 ∠ 149° w/r +x
Which obviously is not in component form, but I still don't know how they got that magnitude or direction. I did notice that is is close to my answer in the y direction, which makes me feel like maybe x-components cancel here?
Anyways, any help would be appreciated! Thank you.