Calculating Area of Normal Stress: Solving for σBC in a Thin Rectangular Rod

Click For Summary

Discussion Overview

The discussion revolves around calculating the area of normal stress for a thin rectangular rod with a hole, specifically focusing on the calculation of σBC. Participants are exploring the dimensions involved in the area calculation and the implications of different views of the rod.

Discussion Character

  • Homework-related
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant questions how the area is derived as (20mm)(40mm-25mm) = 300x10^-6 (m^2) and expresses confusion over the dimensions involved.
  • Another participant explains that the area calculation involves subtracting the hole's width from the total width of the rod and multiplying by the thickness.
  • There are requests for diagrams to visualize the rod and its dimensions, indicating difficulty in understanding the 2D representations.
  • Some participants suggest that the thickness of the rod is 20mm and that it should be considered in the area calculation.
  • Discussions arise about the significance of viewing the rod from different perspectives (top view vs. front view) and how this affects the understanding of normal stress.
  • Participants express uncertainty about the correct cross-sectional area to use for calculations, particularly regarding the circular section of the rod.
  • There is a debate about the correct interpretation of the dimensions provided in the diagrams, with some participants asserting that the diameter of the circular part is not the same as the rod's dimensions.

Areas of Agreement / Disagreement

Participants do not reach a consensus on the correct interpretation of the dimensions and the area calculation. Multiple competing views remain regarding the appropriate cross-sectional area to consider and how to visualize the rod's geometry.

Contextual Notes

There are limitations in the participants' understanding of the diagrams, leading to confusion about the dimensions and how they relate to the area calculations. The discussion reflects varying levels of familiarity with technical drawing and mechanical engineering concepts.

chetzread
Messages
798
Reaction score
1

Homework Statement


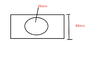
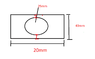
For σBC end , i don't understand how the author get (20mm)(40mm-25mm) = 300x10^-6 (m^2) ...

Homework Equations

The Attempt at a Solution


IMO, , the area should be the circled part (thin rectangular part of the rod) , but i only know one dimension only , which is 40mm , i don't know the another one , how to proceed ?
 

Attachments

  • 0000.PNG
    0000.PNG
    62.1 KB · Views: 695
  • 0001.PNG
    0001.PNG
    31.4 KB · Views: 621
Physics news on Phys.org
Bump
 
40mm - 25mm is the material either side of the hole.
The rod end is 40 wide, less 25 mm for the material missing due to the hole.
This is then multiplied by the rod thickness.
This is the area of the two rectangles we would see if we cut the rod parallel to the end face and coincident with the pin centre line.
 
I
billy_joule said:
40mm - 25mm is the material either side of the hole.
The rod end is 40 wide, less 25 mm for the material missing due to the hole.
This is then multiplied by the rod thickness.
This is the area of the two rectangles we would see if we cut the rod parallel to the end face and coincident with the pin centre line.
I still can't visualize it... Can you help to draw out diagram? The thickness is 20?
 
The thickness (and pin diameter) is shown on the plan view just above your circled diagram.

It's just a rectangular prism with a round hole in it, try draw your own diagram, post it if you get stuck.
 
  • Like
Likes   Reactions: chetzread
billy_joule said:
The thickness (and pin diameter) is shown on the plan view just above your circled diagram.

It's just a rectangular prism with a round hole in it, try draw your own diagram, post it if you get stuck.
i still couldn't imagine , isn't the circle part represent the area ? in the diagram just above my circled part , i didnt see where is the (40-25mm)
Can you explain further ?
 
Can you see how the two diagrams show two views of the same assembly?
Sketch a rectangular prism with a round hole (the rod end) include all the dimensions given, post the drawing.

I assume you're studying mechanical engineering? You haven't done any technical drawing or CAD yet? You'll be expected to interpret drawings of much more complex parts and assemblies and also produce your own drawings, if you're having trouble with this simple part I'd recommend that you start practicing now so you're prepared.
 
  • Like
Likes   Reactions: chetzread
billy_joule said:
Can you see how the two diagrams show two views of the same assembly?
Sketch a rectangular prism with a round hole (the rod end) include all the dimensions given, post the drawing.

I assume you're studying mechanical engineering? You haven't done any technical drawing or CAD yet? You'll be expected to interpret drawings of much more complex parts and assemblies and also produce your own drawings, if you're having trouble with this simple part I'd recommend that you start practicing now so you're prepared.
like this ? I am not sure though .
 

Attachments

  • Untitled.png
    Untitled.png
    5.2 KB · Views: 439
Yes, that's right. If you project backwards you can show the thickness too.

How much material is left either side of the hole to support any loading?
Can you see the significance of 40mm - 25mm now?
 
  • Like
Likes   Reactions: chetzread
  • #10
billy_joule said:
Yes, that's right. If you project backwards you can show the thickness too.

How much material is left either side of the hole to support any loading?
Can you see the significance of 40mm - 25mm now?
the total of 2 red part i add now represent 40 - 25 mm , but where is the 20mm? i didnt see it
 
  • #11
The 20mm dimension is next to the 25mm dimension.
It's given for the fixed support but it's fair to assume they're both the same thickness.
 
  • Like
Likes   Reactions: chetzread
  • #12
billy_joule said:
Yes, that's right. If you project backwards you can show the thickness too.

How much material is left either side of the hole to support any loading?
Can you see the significance of 40mm - 25mm now?
the diagram is confusing ... From the top view , i found that the rod is quite thick (green line represent the thickness) , However , when we view it from front , it is a flat tod ( very thin) . Or you can draw me a 3d diagram please?
 
Last edited:
  • #13
t
billy_joule said:
The 20mm dimension is next to the 25mm dimension.
It's given for the fixed support but it's fair to assume they're both the same thickness.
do you mean here ( in the photo attached) represent 20mm ? if so , it doesn't make sense , right? Since the diameter of circle already = 25mm , which is > 20mm
 

Attachments

  • Untitled.png
    Untitled.png
    7.5 KB · Views: 466
  • #14
billy_joule said:
The 20mm dimension is next to the 25mm dimension.
It's given for the fixed support but it's fair to assume they're both the same thickness.
Can you label in my diagram that i sketched , where is the 20mm ?
 
  • #15
Bump
 
  • #16
chetzread said:
Can you label in my diagram that i sketched , where is the 20mm ?
It's the depth,or thickness of the rod end, into (or out of) the page.
It can't be shown on your sketch as it is only 2D.
 
  • #17
billy_joule said:
It's the depth,or thickness of the rod end, into (or out of) the page.
It can't be shown on your sketch as it is only 2D.
Since it can't be shown on my diagram , then is my diagram wrong ? in the notes , the area is (20)(40-25) .. did I sketch the diagram wrongly?

Or , if my diagram correct ? If so , then it's side view , right ?
 
  • #18
Your first sketch is right, you just need a top (or bottom, or end) view to show depth.
Alternatively, you can do an isometric sketch to show all the information.
You're looking for the area of the two cross hatched sections:
Gy_Jw5qCEOf8Ti1UfmUGkKcJfmSH4xOauYBuYh0TYXbFlum00Ul6lvKJhweo6r-qFwJD7yn_7Hi4i8Wvtzp=w580-h676-no.png
Note that we've taken the authors word that this is the smallest cross sectional area of the rod.
[EDIT: Actually, they do show it's the case]
It is, but only by a very small margin, if the hole size was reduced to 24mm it wouldn't be the area we need to consider.
In future, you'll need to prove that you're using the correct cross section.
 
Last edited:
  • Like
Likes   Reactions: chetzread
  • #19
billy_joule said:
Your first sketch is right, you just need a top (or bottom, or end) view to show depth.
Alternatively, you can do an isometric sketch to show all the information.
You're looking for the area of the two cross hatched sections:
Gy_Jw5qCEOf8Ti1UfmUGkKcJfmSH4xOauYBuYh0TYXbFlum00Ul6lvKJhweo6r-qFwJD7yn_7Hi4i8Wvtzp=w580-h676-no.png
Note that we've taken the authors word that this is the smallest cross sectional area of the rod.
It is, but only by a very small margin, if the hole size was reduced to 24mm it wouldn't be the area we need to consider.
In future, you'll need to prove that you're using the correct cross section.
why we need to consider the stress for the area of side view ? Why not from front view ?
 
  • #20
chetzread said:
why we need to consider the stress for the area of side view ? Why not from front view ?

What is the definition of normal stress?
 
  • Like
Likes   Reactions: chetzread
  • #21
billy_joule said:
What is the definition of normal stress?
stress perpendicular to area
 
  • #22
chetzread said:
why we need to consider the stress for the area of side view ? Why not from front view ?
I'm not sure what you're calling side or front view.
In a uniaxially loaded member there's only one plane with normal stress (or any stress at all).
 
  • Like
Likes   Reactions: chetzread
  • #23
billy_joule said:
I'm not sure what you're calling side or front view.
In a uniaxially loaded member there's only one plane with normal stress (or any stress at all).
Well, new question here . how to get the circular cross section = 314x10^-6 (m^2) ?
i only get 0.5x0.25pi[(25x10^-3) ^2 ][20x10^-3) = (4.91x10^-6)m^2
 
  • #24
chetzread said:
Well, new question here . how to get the circular cross section = 314x10^-6 (m^2) ?
It's the cross sectional area of the circular part of the rod.

i only get 0.5x0.25pi[(25x10^-3) ^2 ][20x10^-3) = (4.91x10^-6)m^2
I have no idea what you're doing trying to do there.

What is the diameter of the circular part of the rod? So what is it's cross sectional area?
 
  • #25
billy_joule said:
It's the cross sectional area of the circular part of the rod.I have no idea what you're doing trying to do there.

What is the diameter of the circular part of the rod? So what is it's cross sectional area?
diameter = 25mm ,
thus , cross sectional area = 0.25pi[(25x10^-3) ^2 ] = 4.91x10^-4 (m^2) ?
 
  • #26
chetzread said:
diameter = 25mm ,

Nope.
The pins have a 25mm OD, not the rod.
 
  • #27
billy_joule said:
Nope.
The pins have a 25mm OD, not the rod.
Then , what should it be ?
 
  • #28
chetzread said:
Then , what should it be ?
Come on, It's shown two times on your first attachment! it's even labeled with a 'd' so you know its a diameter of a circular section!

Interpreting the diagrams in this question should only take a few seconds, if you want to pass your exams you'll need to seriously improve your skill in this area.
I strongly suggest you follow my advice in post #7.
 
  • Like
Likes   Reactions: chetzread

Similar threads

Understanding the Difference Between Bending Stress and Normal Stress in Beams
  • · Replies 6 ·
Replies
6
Views
2K
Stress on a spaghetti rod balanced from its middle
  • · Replies 6 ·
Replies
6
Views
1K
What is the Correct Calculation for Stress in Steel and Concrete?
  • · Replies 11 ·
Replies
11
Views
3K
How Does Biaxial Force Affect Stress and Strain in a Rectangular Bar?
  • · Replies 1 ·
Replies
1
Views
2K
Cross Sectional Area, Stress and Strain confusion
  • · Replies 5 ·
Replies
5
Views
17K
Stress & Strain: Calculate Forces, Diameters & Lengths
  • · Replies 3 ·
Replies
3
Views
5K
Elasticity: Determine zero normal stress plane
  • · Replies 1 ·
Replies
1
Views
2K
Static B.C & first moment of area of connecting rod
  • · Replies 4 ·
Replies
4
Views
2K
Calculating stress and strains for beam of applied force
  • · Replies 1 ·
Replies
1
Views
2K
Finding the Force P from Normal Stress
  • · Replies 3 ·
Replies
3
Views
6K